题目内容
6.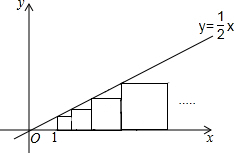 如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.
如图,在直线y=$\frac{1}{2}$x的下方依次作小正方形,每个小正方形的一个顶点都在直线y=$\frac{1}{2}$x上,若最小的正方形左边顶点的横坐标是1,则从左到右第10个小正方形的边长是$\frac{19683}{1024}$.
分析 设第n个正方形的边长为an(n为正整数),根据题意罗列出部分an的值,根据数据的变化找出变化规律“an=$\frac{1}{2}$×$(\frac{3}{2})^{n-1}$=$\frac{{3}^{n-1}}{{2}^{n}}$”,依据此规律即可得出结论.
解答 解:设第n个正方形的边长为an(n为正整数),
观察,发现规律:a1=$\frac{1}{2}$,a2=a1+$\frac{1}{2}$a1=$\frac{3}{2}$a1=$\frac{3}{4}$,a3=a2+$\frac{1}{2}$a2=$\frac{3}{2}$a2=$\frac{9}{8}$,a4=a3+$\frac{1}{2}$a3=$\frac{3}{2}$a3=$\frac{27}{16}$,…,
∴an=$\frac{1}{2}$×$(\frac{3}{2})^{n-1}$=$\frac{{3}^{n-1}}{{2}^{n}}$.
当n=10时,a10=$\frac{{3}^{9}}{{2}^{10}}$=$\frac{19683}{1024}$.
故答案为:$\frac{19683}{1024}$.
点评 本题考查了一次函数图象上点的坐标特征以及规律型中得图形的变化规律,解题的关键是找出规律“an=$\frac{1}{2}$×$(\frac{3}{2})^{n-1}$=$\frac{{3}^{n-1}}{{2}^{n}}$”.本题属于基础题,难度不大,解决该题型题目时,根据给定的条件罗列出部分正方形的边长,根据数据的变化找出变化规律是关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
16.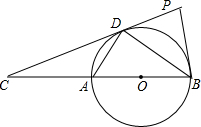 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
17. 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
1.下列运算正确的是( )
| A. | 4a-a=3 | B. | a6÷a3=a3 | C. | (ab)2=ab2 | D. | (a-b)2=a2-b2 |
7.在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )
| A. | a=5,b=13,c=12 | B. | a=11,b=12,c=15 | C. | a:b:c=3:4:5 | D. | a=b=1,c=$\sqrt{2}$ |
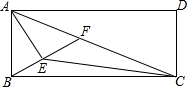 如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.
如图,在矩形ABCD中,AB=5,AD=12,AC是它的一条对角线,AE平分∠BAC,BE⊥AE于点E,交AC于点F,连接CE,则四边形AECD的面积是45.