题目内容
如图1,在△ABC中,∠BAC=90°,AB=AC,AO⊥BC于点O,F是线段AO上的点(与A、O不重合),∠EAF=90°,AE=AF,连接FE,FC,BF.
(1)求证:BE=BF;
(2)如图2,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①判断线段CF与BE的关系,并说明理由.
②当△BEF为等腰直角三角形时,请直接写出AB:BF的值.

(1)求证:BE=BF;
(2)如图2,若将△AEF绕点A旋转,使边AF在∠BAC的内部,延长CF交AB于点G,交BE于点K.
①判断线段CF与BE的关系,并说明理由.
②当△BEF为等腰直角三角形时,请直接写出AB:BF的值.

考点:旋转的性质,全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)通过证明△EAB≌△FAB,即可得到BE=BF;
(2)①首先证明△AEB≌△AFC,可得CF=BE.
②由全等三角形的性质可得:∠EBA=∠FCA,进而可证明△AGC∽△KGB,因为△AGC∽△KGB,所以∠GKB=∠GAC=90°,所以∠EBF<90°,由此可分两种情况讨论求值即可.
(2)①首先证明△AEB≌△AFC,可得CF=BE.
②由全等三角形的性质可得:∠EBA=∠FCA,进而可证明△AGC∽△KGB,因为△AGC∽△KGB,所以∠GKB=∠GAC=90°,所以∠EBF<90°,由此可分两种情况讨论求值即可.
解答:解;(1)证明:∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,
∴∠EAB=∠BAF,
在△EAB和△FAB中,
,
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①CF=BE.
证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
,
∴△AEB≌△AFC(SAS),
∴CF=BE;
②∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
∴∠GKB=∠GAC=90°,
∴∠EBF<90°,
当∠EFB=90°时,
设AE=x,
∵∠EAF=90°,AE=AF,
∴EF=
x,
∵△BEF为等腰直角三角形,
∴BF=EF=
x,∠FBE=45°.
∴BE=2x
又∵∠EAF=90°,AE=AF,
∴∠AEF=45°.
∴∠AEB=90°.
∴AB=
=
x,
AB:BF=
x:
x=
:
.
同理,当∠BEF=90°,此时AB:BF=
:2.
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,
∴∠EAB=∠BAF,
在△EAB和△FAB中,
|
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①CF=BE.
证明:∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
|
∴△AEB≌△AFC(SAS),
∴CF=BE;
②∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
∴∠GKB=∠GAC=90°,
∴∠EBF<90°,
当∠EFB=90°时,
设AE=x,
∵∠EAF=90°,AE=AF,
∴EF=
| 2 |
∵△BEF为等腰直角三角形,
∴BF=EF=
| 2 |
∴BE=2x
又∵∠EAF=90°,AE=AF,
∴∠AEF=45°.
∴∠AEB=90°.
∴AB=
| AE2+BE2 |
| 5 |
AB:BF=
| 5 |
| 2 |
| 5 |
| 2 |
同理,当∠BEF=90°,此时AB:BF=
| 5 |
点评:本题考查了全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的性质,题目的综合性很强,难度不小,对学生的解题能力要求很高.

练习册系列答案
相关题目
开元商场把进价为1875元的某商品按标价的九折出售,仍获利20%,则该商品的标价为( )
| A、2000元 |
| B、2500元 |
| C、2800元 |
| D、3000元 |
 如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化.
如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化.
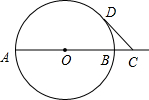 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA. 如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为60°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=30°,且D、A、C在同一条直线上,求塔BD的高度(测角仪的高度忽略不计,结果用根号表示)
如图,某人在山脚A处测得一座塔BD的塔尖点B的仰角为60°,沿山坡向上走到P处再测得点B的仰角为45°,已知坡面AP=40米,坡角∠PAC=30°,且D、A、C在同一条直线上,求塔BD的高度(测角仪的高度忽略不计,结果用根号表示)
 如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为
如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的面积为