题目内容
如图1,已知抛物线y=ax2+bx+c(a≠0)经过A(3,0)、B(4,4)两点.
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,求点N的坐标;
(4)在(2)与(3)的条件下,请直接写出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应).

(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,求点N的坐标;
(4)在(2)与(3)的条件下,请直接写出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应).

考点:二次函数综合题
专题:
分析:(1)利用待定系数法求二次函数解析式进而得出答案即可;
(2)根据已知条件可求出OB的解析式为y=x,则向下平移m个单位长度后的解析式为:y=x-m.由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标;
(3)设点N(n,
n+3),又点N在抛物线y=x2-3x上,代入抛物线的解析式即可求出n的值,进而得到N的坐标;
(4)首先求出直线A′B的解析式,进而由△P1OD∽△NOB,得出△P1OD∽△N1OB1,进而求出点P1的坐标,再利用翻折变换的性质得出另一点的坐标.
(2)根据已知条件可求出OB的解析式为y=x,则向下平移m个单位长度后的解析式为:y=x-m.由于抛物线与直线只有一个公共点,意味着联立解析式后得到的一元二次方程,其根的判别式等于0,由此可求出m的值和D点坐标;
(3)设点N(n,
| 1 |
| 4 |
(4)首先求出直线A′B的解析式,进而由△P1OD∽△NOB,得出△P1OD∽△N1OB1,进而求出点P1的坐标,再利用翻折变换的性质得出另一点的坐标.
解答:解:(1)∵抛物线y=ax2+bx(a≠0)经过A(3,0)、B(4,4)
∴将A与B两点坐标代入得:
,
解得:
.
∴抛物线的解析式是y=x2-3x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,
解得:k1=1.
∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=x-m,
∵点D在抛物线y=x2-3x上,
∴可设D(x,x2-3x),
又∵点D在直线y=x-m上,
∴x2-3x=x-m,即x2-4x+m=0,
∵抛物线与直线只有一个公共点,
∴△=16-4m=0,
解得:m=4,
此时x1=x2=2,y=x2-3x=-2,
∴D点的坐标为(2,-2).
(3)∵直线OB的解析式为y=x,且A(3,0),
∴点A关于直线OB的对称点A′的坐标是(0,3),
根据轴对称性质和三线合一性质得出∠A′BO=∠ABO,
设直线A′B的解析式为y=k2x+3,过点(4,4),
∴4k2+3=4,解得:k2=
,
∴直线A′B的解析式是y=
x+3,
∵∠NBO=∠ABO,∠A′BO=∠ABO,
∴BA′和BN重合,
即点N在直线A′B上,
∴设点N(n,
n+3),又点N在抛物线y=x2-3x上,
∴
=n2-3n,
解得:n1=-
,n2=4(不合题意,舍去)
∴N点的坐标为(-
,
).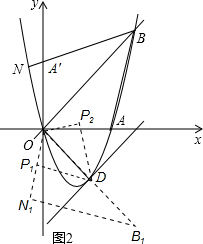
(4)如图,将△NOB沿x轴翻折,得到△N1OB1,
由(3)可知:N1 (-
,-
),B1(4,-4).
∴O、D、B1都在直线y=-x上.
过D点做DP1∥N1B1,
∵△P1OD∽△NOB,
∴△P1OD∽△N1OB1,
∴P1为O N1的中点.
∴
=
,
∴点P1的坐标为(-
,-
).
将△P1OD沿直线y=-x翻折,可得另一个满足条件的点到x轴距离等于P1到y轴距离,点到y轴距离等于P1到x轴距离,
∴此点坐标为:(
,
).
综上所述,点P的坐标为(-
,-
)和(
,
).
∴将A与B两点坐标代入得:
|
解得:
|
∴抛物线的解析式是y=x2-3x.
(2)设直线OB的解析式为y=k1x,由点B(4,4),
得:4=4k1,
解得:k1=1.
∴直线OB的解析式为y=x,
∴直线OB向下平移m个单位长度后的解析式为:y=x-m,
∵点D在抛物线y=x2-3x上,
∴可设D(x,x2-3x),
又∵点D在直线y=x-m上,
∴x2-3x=x-m,即x2-4x+m=0,
∵抛物线与直线只有一个公共点,
∴△=16-4m=0,
解得:m=4,
此时x1=x2=2,y=x2-3x=-2,
∴D点的坐标为(2,-2).
(3)∵直线OB的解析式为y=x,且A(3,0),
∴点A关于直线OB的对称点A′的坐标是(0,3),
根据轴对称性质和三线合一性质得出∠A′BO=∠ABO,
设直线A′B的解析式为y=k2x+3,过点(4,4),
∴4k2+3=4,解得:k2=
| 1 |
| 4 |
∴直线A′B的解析式是y=
| 1 |
| 4 |
∵∠NBO=∠ABO,∠A′BO=∠ABO,
∴BA′和BN重合,
即点N在直线A′B上,
∴设点N(n,
| 1 |
| 4 |
∴
| 1 |
| 4 |
解得:n1=-
| 3 |
| 4 |
∴N点的坐标为(-
| 3 |
| 4 |
| 45 |
| 16 |

(4)如图,将△NOB沿x轴翻折,得到△N1OB1,
由(3)可知:N1 (-
| 1 |
| 4 |
| 45 |
| 16 |
∴O、D、B1都在直线y=-x上.
过D点做DP1∥N1B1,
∵△P1OD∽△NOB,
∴△P1OD∽△N1OB1,
∴P1为O N1的中点.
∴
| OP1 |
| ON |
| OD |
| OB1 |
∴点P1的坐标为(-
| 3 |
| 8 |
| 45 |
| 32 |
将△P1OD沿直线y=-x翻折,可得另一个满足条件的点到x轴距离等于P1到y轴距离,点到y轴距离等于P1到x轴距离,
∴此点坐标为:(
| 45 |
| 32 |
| 3 |
| 8 |
综上所述,点P的坐标为(-
| 3 |
| 8 |
| 45 |
| 32 |
| 45 |
| 32 |
| 3 |
| 8 |
点评:本题是基于二次函数的代数几何综合题,综合考查了待定系数法求抛物线解析式、一次函数(直线)的平移、一元二次方程根的判别式、翻折变换、旋转变换以及相似三角形等重要知识点.本题将初中阶段重点代数、几何知识熔于一炉,难度很大,对学生能力要求极高,具有良好的区分度,是一道非常好的中考压轴题.

练习册系列答案
相关题目
若x=-1是方程
-
=0的根,则( )
| a |
| x-1 |
| 3 |
| x |
| A、a=6 | B、a=-6 |
| C、a=3 | D、a=-3 |
对于数据组3,3,2,3,6,3,10,3,6,3,2.这组数据的平均数与众数分别为( )
| A、4,3 | B、3,3 |
| C、4.5,2 | D、5,6 |

 如图,点A是直线y=2x上一动点,以A为顶点的抛物线y=(x-m)2+h交直线y=2x于另一点E,交y轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C(点A,E,F两两不重合).
如图,点A是直线y=2x上一动点,以A为顶点的抛物线y=(x-m)2+h交直线y=2x于另一点E,交y轴于点F,抛物线的对称轴交x轴于点B,交直线EF于点C(点A,E,F两两不重合).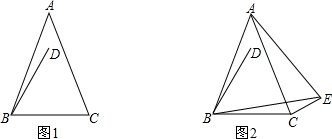
 △ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB=
△ABC中,D在BC上,且AB=AC=BD,∠1=30°,∠ADB=