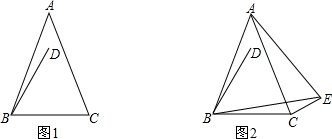题目内容
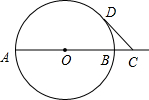 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.(1)当OC=2
| 2 |
(2)当OC>2
| 2 |
考点:切线的判定
专题:动点型
分析:(1)直接利用勾股定理的逆定理进而得出△ODC是直角三角形,求出CD是切线即可;
(2)利用等边三角形的判定以及勾股定理分别求出AE,CO的长,进而得出答案.
(2)利用等边三角形的判定以及勾股定理分别求出AE,CO的长,进而得出答案.
解答: (1)证明:连接DO,
(1)证明:连接DO,
∵AB是⊙O的直径,AB=4,CD=OA,
∴CD=OD=2,
∴DO2+CD2=CO2,
∴△ODC是直角三角形,
∴∠ODC=90°,
∴CD是⊙O的切线;
(2)解:如图2,连接EO,DO,
∵D为CE中点,CD=OA,
∴EO=DO=CD=DE,
∴△EOD是等边三角形,
∵DO=ED=CD,
∴△EOC是直角三角形,
∴∠AOE=∠EOC=90°,
∴AE=
=2
,OC=
=2
,
∴△ACE的周长为:AE+EC+AC=2
+4+2
+2=6+2
+2
.
 (1)证明:连接DO,
(1)证明:连接DO,∵AB是⊙O的直径,AB=4,CD=OA,
∴CD=OD=2,
∴DO2+CD2=CO2,
∴△ODC是直角三角形,
∴∠ODC=90°,
∴CD是⊙O的切线;
(2)解:如图2,连接EO,DO,
∵D为CE中点,CD=OA,

∴EO=DO=CD=DE,
∴△EOD是等边三角形,
∵DO=ED=CD,
∴△EOC是直角三角形,
∴∠AOE=∠EOC=90°,
∴AE=
| 22+22 |
| 2 |
| EC2-EO2 |
| 3 |
∴△ACE的周长为:AE+EC+AC=2
| 2 |
| 3 |
| 2 |
| 3 |
点评:此题主要考查了勾股定理以及切线的判定等知识,得出∠EOC=90°是解题关键.

练习册系列答案
相关题目
下列条件一定能推得△ABC与△DEF全等的是( )
| A、在△ABC和△DEF中,∠A=∠B,∠D=∠E,AB=DE | ||||
| B、在△ABC和△DEF中,AB=AC,∠A=∠F,FD=FE | ||||
C、在△ABC和△DEF中,
| ||||
D、在△ABC和△DEF中,
|
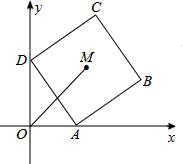 在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为
在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为