题目内容
 如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化.
如图,一个四棱柱的底面是一个边长为10cm的正方形,它的高变化时,棱柱的体积也发生变化.(1)在这个变化中,自变量为
(2)如果高为h(cm)时,体积为V(cm3),则V与h的关系为
(3)当高为5cm时,棱柱体积为
(4)棱柱的高由1cm变到5cm时,体积由
考点:函数关系式,常量与变量,函数值
专题:
分析:(1)在这个变化中,棱柱的体积随着高的变化而变化可知自变量、因变量;
(2)根据棱柱的体积公式:V=Sh可得答案;
(3)利用待定系数法把高为5cm代入函数关系式即可;
(4)利用待定系数法把高为1cm代入函数关系式,高为5cm代入函数关系式计算即可.
(2)根据棱柱的体积公式:V=Sh可得答案;
(3)利用待定系数法把高为5cm代入函数关系式即可;
(4)利用待定系数法把高为1cm代入函数关系式,高为5cm代入函数关系式计算即可.
解答:解:(1)∵它的高变化时,棱柱的体积也随着变化.
∴自变量、因变量分别是:高,体积;
(2)高为h(cm)时,体积为V(cm3),则V与h的关系为:V=100h;
(3)当高为5cm时,棱柱的体积是:500cm3;
(4)棱柱的高由1cm变化到10cm时,它的体积由 100cm3变化到500cm3.
故答案为:①高,体积;②v=100h;③500cm3;④100变化到500.
∴自变量、因变量分别是:高,体积;
(2)高为h(cm)时,体积为V(cm3),则V与h的关系为:V=100h;
(3)当高为5cm时,棱柱的体积是:500cm3;
(4)棱柱的高由1cm变化到10cm时,它的体积由 100cm3变化到500cm3.
故答案为:①高,体积;②v=100h;③500cm3;④100变化到500.
点评:此题主要考查了列函数关系式,求函数值,题目比较简单,代数时认真一些,然后计算即可.

练习册系列答案
相关题目
在△ABC中,已知∠A=3∠C=54°,则∠B的度数是( )
| A、90° | B、94° |
| C、98° | D、108° |
若x=-1是方程
-
=0的根,则( )
| a |
| x-1 |
| 3 |
| x |
| A、a=6 | B、a=-6 |
| C、a=3 | D、a=-3 |
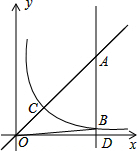 如图,B为双曲线y=
如图,B为双曲线y=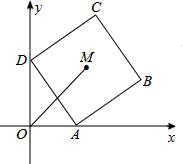 在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为
在平面直角坐标系中,如图,点A的坐标是(2,0),点D在y轴的正半轴上,以线段AD为边向外作正方形ABCD如图所示,该正方形的中心M(3,3),那么点D的坐标为