题目内容
如图1,矩形ABCD中,点P从A出发,以3cm/s的速度沿边A→B→C→D→A匀速运动;同时点Q从B出发,沿边B→C→D匀速运动,当其中一个点到达终点时两点同时停止运动,设点P运动的时间为t s.△APQ的面积s(cm2)与t(s)之间函数关系的部分图象由图2中的曲线段OE与线段EF给出.
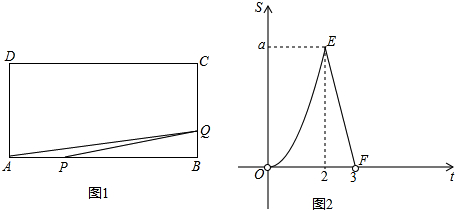
(1)点Q运动的速度为 cm/s,a﹦ cm2;
(2)若BC﹦3cm,
①求t>3时S的函数关系式;
②在图(2)中画出①中相应的函数图象.

(1)点Q运动的速度为
(2)若BC﹦3cm,
①求t>3时S的函数关系式;
②在图(2)中画出①中相应的函数图象.
考点:二次函数综合题,动点问题的函数图象
专题:压轴题
分析:(1)根据点E时S最大,判断出2秒时点P运动至点B,点Q运动至点C,然后根据点P的速度求出AB,再根据3秒时,S=0判断出点P与点Q重合,然后根据追击问题的等量关系列出方程求出点Q的速度即可得解;
(2)①求出3秒时点P、Q在点C重合,再求出点P到达点D的时间为5秒,到达点A的时间为6秒,然后分3<t≤5时表示出PQ,然后根据三角形的面积公式列式整理即可;5<t≤6时,表示出AP、DQ,然后利用三角形的面积公式列式整理即可;
②根据函数解析式作出图象即可.
(2)①求出3秒时点P、Q在点C重合,再求出点P到达点D的时间为5秒,到达点A的时间为6秒,然后分3<t≤5时表示出PQ,然后根据三角形的面积公式列式整理即可;5<t≤6时,表示出AP、DQ,然后利用三角形的面积公式列式整理即可;
②根据函数解析式作出图象即可.
解答:解:(1)由图可知,2秒时点P运动至点B,点Q运动至点C,
∵点P的速度为3cm/s,
∴AB=3×=6cm,
3秒时,S=0判断出点P与点Q重合,
设点Q的速度为xcm/s,
则3x+6=3×3,
解得x=1,
此时,BC=2×1=2cm,
a=
×6×2=6cm2,
故答案为:1,6;
(2)∵(6+3)÷3=3s,3÷1=3s,
∴3秒时点P、Q在点C重合,
点P到达点D的时间为:(6+3+6)÷3=5s
到达点A的时间为:(6+3+6+3)÷3=6s,
①若3<t≤5,则PQ=3t-t-6=2t-6,
S=
×(2t-6)×3=3t-9;
若5<t≤6,则AP=(6+3+6+3)-3t=18-3t,
DQ=(6+3)-t=9-t,
S=
×(18-3t)×(9-t)=
t2-
t+81;
所以,S=
;
②函数图象如图2所示.
∵点P的速度为3cm/s,
∴AB=3×=6cm,
3秒时,S=0判断出点P与点Q重合,
设点Q的速度为xcm/s,
则3x+6=3×3,
解得x=1,
此时,BC=2×1=2cm,
a=
| 1 |
| 2 |
故答案为:1,6;
(2)∵(6+3)÷3=3s,3÷1=3s,
∴3秒时点P、Q在点C重合,
点P到达点D的时间为:(6+3+6)÷3=5s
到达点A的时间为:(6+3+6+3)÷3=6s,

①若3<t≤5,则PQ=3t-t-6=2t-6,
S=
| 1 |
| 2 |
若5<t≤6,则AP=(6+3+6+3)-3t=18-3t,
DQ=(6+3)-t=9-t,
S=
| 1 |
| 2 |
| 3 |
| 2 |
| 45 |
| 2 |
所以,S=
|
②函数图象如图2所示.
点评:本题是二次函数综合题型,动点问题函数图象,主要利用了路程、速度、时间三者之间的关系,根据图2判断出2秒时点P、Q的位置是解题的关键,也是本题的难点,根据3秒时,点P、Q重合利用追击问题等量关系求出点Q的速度也很重要.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
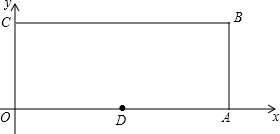 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
 如图,矩形ABCD中,AB=2
如图,矩形ABCD中,AB=2