题目内容
如图,已知AB∥CD∥EF∥GH.
(1)如图1,M是直线EF上的点,写出∠BAM、∠AMC和∠MCD的数量关系,并证明你的结论;
(2)如图2,点M,N分别是直线EF,CH上的动点,画出图形,并直接写出四个角∠BAM,∠AMN,∠MNC,∠NCD之间的等量关系.
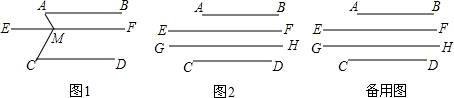
(1)如图1,M是直线EF上的点,写出∠BAM、∠AMC和∠MCD的数量关系,并证明你的结论;
(2)如图2,点M,N分别是直线EF,CH上的动点,画出图形,并直接写出四个角∠BAM,∠AMN,∠MNC,∠NCD之间的等量关系.

考点:平行线的性质
专题:
分析:(1)根据两直线平行,内错角相等可得∠BAM=∠AME,∠EMC=∠MCD,然后根据∠AMC=∠AME+∠EMC等量代换即可得解;
(2)根据点M、N的位置,分四种情况作出图形,然后根据平行线的性质写出关系式即可.
(2)根据点M、N的位置,分四种情况作出图形,然后根据平行线的性质写出关系式即可.
解答: 解:(1)∠AMC=∠BAM+∠MCD.
解:(1)∠AMC=∠BAM+∠MCD.
理由为:∵AB∥EF,
∴∠BAM=∠AME,
∵EF∥CD,
∴∠EMC=∠MCD,
∴∠AMC=∠AME+∠EMC=∠BAM+∠MCD;
(2)如图①,∠BAM+∠AMN+∠MNC+∠NCD=540°;
如图②,∠BAM+∠AMN+∠NCD=∠MNC+180°;
如图③,∠BAM+∠MNC+∠NCD=∠AMN+180°,
如图④,∠AMN+∠MNC=∠BAM+∠NCD+180°.
 解:(1)∠AMC=∠BAM+∠MCD.
解:(1)∠AMC=∠BAM+∠MCD.理由为:∵AB∥EF,
∴∠BAM=∠AME,
∵EF∥CD,
∴∠EMC=∠MCD,
∴∠AMC=∠AME+∠EMC=∠BAM+∠MCD;
(2)如图①,∠BAM+∠AMN+∠MNC+∠NCD=540°;
如图②,∠BAM+∠AMN+∠NCD=∠MNC+180°;
如图③,∠BAM+∠MNC+∠NCD=∠AMN+180°,
如图④,∠AMN+∠MNC=∠BAM+∠NCD+180°.
点评:此题考查了平行线的性质,熟练掌握平行线的性质是解本题的关键,难点在于(2)分情况讨论.

练习册系列答案
相关题目
已知:1-(3m-5)2有最大值,则方程5m-4=3x+2的解是( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2
如图,已知△ABC在平面直角坐标系中,其中点A、B、C三点的坐标分别为(1,2 如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.
如图,已知:∠ADC=∠ABC,DE,BF分别是两个角的平分线,且∠AED=∠ABF.求证:AB∥CD.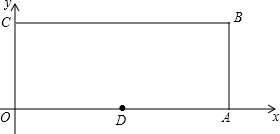 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是的OA中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.