题目内容
10.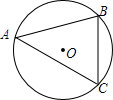 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
分析 过A点作直径AD,则∠ABD=90°,∠ADB=∠ACB=60°,在Rt△ABD中,AB=3cm,利用三边的数量关系可求出AD.
解答 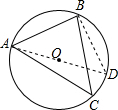 解:过A点作直径AD,连接BD,如图,
解:过A点作直径AD,连接BD,如图,
∠ABD=90°,
又∵∠ADB=∠ACB=60°,
∴∠BAD=30°,
∵AB=3cm,
∴BD=$\frac{AB}{tan60°}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴AD=2BD=2$\sqrt{3}$(cm),
即⊙O的直径为 2$\sqrt{3}$cm.
故答案为:2$\sqrt{3}$.
点评 本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了直径所对的圆周角为90度和勾股定理.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
2.如果一元二次方程x2+12x+27=0的两个根是x1,x2,那么x1+x2的值为( )
| A. | -6 | B. | -12 | C. | 12 | D. | 27 |
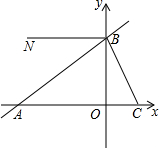 如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.
如图,在坐标系中,直线y=-3x+6与x轴的正半轴交于点C,与y轴的正半轴交于点B,直线BA与x轴的负半轴交于点A,AB=5OC,射线BN∥x轴.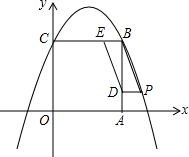 如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C.
如图,在直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在x轴、y轴的正半轴上.抛物线y=-x2+bx+c经过点B、C. 如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证:
如图,⊙O是△ABC的外接圆,弦CD⊥AB,CE是直径,F是弧AB的中点,求证: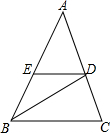 如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.
如图,在△ABC中,AB=AC,BD是∠ABC的平分线,DE∥BC,则CD=DE.请说明理由.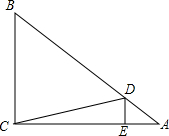 如图,在Rt△ABC中,∠ACB=90°,$sinA=\frac{2}{3}$,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9,求
如图,在Rt△ABC中,∠ACB=90°,$sinA=\frac{2}{3}$,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9,求