题目内容
20.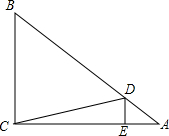 如图,在Rt△ABC中,∠ACB=90°,$sinA=\frac{2}{3}$,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9,求
如图,在Rt△ABC中,∠ACB=90°,$sinA=\frac{2}{3}$,点D、E分别在AB、AC上,DE⊥AC,垂足为点E,DE=2,DB=9,求(1)BC的长;
(2)cos∠BCD.
分析 (1)由三角函数求出AD,DCAB,再由三角函数求出BC即可;
(2)由勾股定理求出AC,得出CE,由勾股定理求出CD,由三角函数求出cos∠CDE,由平行线的性质得出∠CDE=∠BCD,即可得出结果.
解答 解:(1)在Rt△DEA中,
∵DE=2,sinA=$\frac{2}{3}$,
∴$AD=\frac{DE}{sinA}=2×\frac{3}{2}=3$,
∴AB=BD+AD=12,
在Rt△ABC中,AB=12,sinA=$\frac{2}{3}$
∴$BC=AB•sinA=12×\frac{2}{3}=8$;
(2)在Rt△ABC中,AB=12,BC=8,
由勾股定理得:$AC=4\sqrt{5}$,
在Rt△DEA中,DE=2,AD=3
∴$AE=\sqrt{5}$,
∴$CE=4\sqrt{5}-\sqrt{5}=3\sqrt{5}$,
∴CD=$\sqrt{C{D}^{2}+C{E}^{2}}$=7,
在Rt△DEC中,$cos∠CDE=\frac{DE}{CD}=\frac{2}{7}$,
∵DE∥BC,
∴∠CDE=∠BCD
∴$cos∠BCD=cos∠CDE=\frac{2}{7}$.
点评 本题考查了解直角三角形、勾股定理、三角函数;熟练掌握解直角三角形,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列各题中,能用平方差公式计算的是( )
| A. | (a-$\frac{1}{2}$b)(a-$\frac{1}{2}$b) | B. | (a-$\frac{1}{2}$b)(-a+$\frac{1}{2}$b) | C. | (a-$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) | D. | (a+$\frac{1}{2}$b)(-a-$\frac{1}{2}$b) |
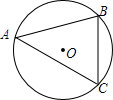 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.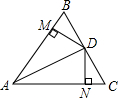 如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.
如图所示,△ABC中,AD平分∠BAC,点D是BC的中点,DM⊥AB,DN⊥AC,垂足分别为M,N,求证:∠B=∠C,BM=CN.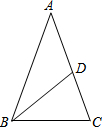 如图,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC,那么CD=$\frac{4}{3}$.
如图,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC,那么CD=$\frac{4}{3}$.