题目内容
4.阅读下面的文字,完成解答过程.(1)$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,则$\frac{1}{2013×2014}$=$\frac{1}{2013}$-$\frac{1}{2014}$,并且用含有n的式子表示你发现的规律$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)根据上述方法计算:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$.
(3)根据(1),(2)的计算,我们可以猜测下列结论:$\frac{1}{n(n+k)}$=$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$)(其中n,k均为正整数),并计算$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{2014×2017}$.
分析 (1)根据观察,可发现规律:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)根据拆项法,可出现互为相反数的项,根据有理数的加法,可得答案;
(3)根据计算,可发现$\frac{1}{n(n+k)}$=$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$),根据规律,可得互为相反数的项,根据有理数的加法,可得答案.
解答 解:(1)$\frac{1}{2013×2014}$=$\frac{1}{2013}$-$\frac{1}{2014}$,并且用含有n的式子表示你发现的规律 $\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{2013}$-$\frac{1}{2014}$)=$\frac{1}{2}$×(1-$\frac{1}{2014}$)=$\frac{1}{2}$×$\frac{2013}{2014}$=$\frac{2013}{4028}$;
(3)$\frac{1}{n(n+k)}$=$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$)(其中n,k均为正整数),
$\frac{1}{1×4}$+$\frac{1}{4×7}$+$\frac{1}{7×10}$+…+$\frac{1}{2014×2017}$=$\frac{1}{3}$×(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{2014}$-$\frac{1}{2017}$)
=$\frac{1}{3}$×(1-$\frac{1}{2017}$)
=$\frac{1}{2}$×$\frac{2016}{2017}$=$\frac{1008}{2017}$,
故答案为:$\frac{1}{2013}$-$\frac{1}{2014}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,$\frac{1}{k}$($\frac{1}{n}$-$\frac{1}{n+k}$).
点评 本题考查了分式的加减,利用拆项法得出互为相反数的项是解题关键.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案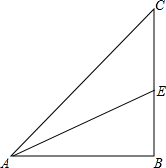 如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E,请你判断一下,甲、乙两人谁先到达各自的目的地?请说明理由.
如图,在Rt△ABC的场地上,∠B=90°,AB=BC,∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发,以相同的速度分别沿AC和A→B→E线路前进,甲的目的地为C,乙的目的地为E,请你判断一下,甲、乙两人谁先到达各自的目的地?请说明理由. 如图,P是⊙O外一点,PA、PB、DE分别与⊙O相切于点A,B,C,PA=a,PB=b.
如图,P是⊙O外一点,PA、PB、DE分别与⊙O相切于点A,B,C,PA=a,PB=b.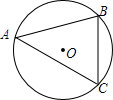 如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.
如图,在⊙O中,弦AB=3cm,圆周角∠ACB=60°,则⊙O的直径等于2$\sqrt{3}$cm.