题目内容
17.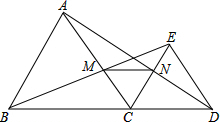 如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:△MNC是等边三角形.
分析 (1)依据等边三角形的性质可得到BE=AD,CE=CD,∠ACB=∠ECD=60°,然后可证明∠ACD=∠BCE=120°,依据SAS可证明△BCE≌△ACD,最后依据全等三角形的性质可得到BE=AD;
(2)证明△BCM≌△ACN,从而得到MC=CN,然后证明∠MCN=60°即可.
解答 解:(1)BE=AD.
理由:∵∠BCA=∠DCE=60°,
∴∠BCE=∠ACD,
在△BCE和△ACD中,$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD(SAS);
∴BE=AD…(4分)
(2)∵△BCE≌△ACD,
∴∠CBM=∠CAN.
∵∠ACB=∠DCE=60°,
∴∠ACN=60°.
∴∠BCM=∠ACN,
在△BCM和△ACN中$\left\{\begin{array}{l}{∠CBM=∠CAN}\\{BC=AC}\\{∠BCM=∠ACN}\end{array}\right.$,
∴△BCM≌△ACN(ASA),
∴CM=CN;
∵∠ACN=60°,
∴△CMN是等边三角形.
点评 本题主要考查的是等边三角形的性质和判定、全等三角形的性质和判定,证得△BCM≌△ACN是解题的关键.

练习册系列答案
相关题目
2.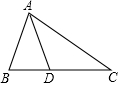 已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
 已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )
已知:如图,在△ABC中,AD是它的角平分线,AB=6cm,AC=8cm,则 S△ABD:S△ACD=( )| A. | 4:3 | B. | 3:4 | C. | 16:9 | D. | 9:16 |
9.下列能使平行四边形ABCD是矩形的条件是( )
| A. | AB=CD | B. | AC⊥BD | C. | ∠ABC=90° | D. | AD=BC |
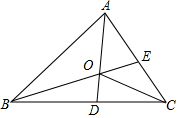 如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断:
如图,AD和BE是△ABC的角平分线且交于点O,连接OC,现有以下论断: 如图,已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,求证:△ABC是等腰三角形.
如图,已知∠EAC是△ABC的外角,∠1=∠2,AD∥BC,求证:△ABC是等腰三角形.