题目内容
解方程时,把某个式子看做整体,用新的未知数去代替它,使方程得到简化,这叫换元法,先阅读下面的解题过程,再解后面的方程:
例:解方程 2
-3=0
解:设
=t,(t≥0)
∴原方程可化为2t-3=0
∴t=
,∴
=
,x=
.
请利用前面的方法,解方程
x+2
-8=0.
例:解方程 2
| x |
解:设
| x |
∴原方程可化为2t-3=0
∴t=
| 3 |
| 2 |
| x |
| 3 |
| 2 |
| 9 |
| 4 |
请利用前面的方法,解方程
x+2
| x |
考点:无理方程
专题:换元法
分析:设
=t,则x=t2,则原方程化为t2+2t-8=0,求出方程的解,即可求出答案.
| x |
解答:解:设
=t,则x=t2,
原方程化为t2+2t-8=0,
解得:t1=-4,t2=2,
当t=-4时,
=-4,此时方程无解,
当t=2时,
=2,
解得:x=4,
经检验x=4是原方程的解,
即原方程的解为x=4.
| x |
原方程化为t2+2t-8=0,
解得:t1=-4,t2=2,
当t=-4时,
| x |
当t=2时,
| x |
解得:x=4,
经检验x=4是原方程的解,
即原方程的解为x=4.
点评:本题考查了用换元法解无理方程的应用,解此题的关键是能把无理方程转化成有理方程,题目比较好,难度适中.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
在三角形ABC中∠A=60°,∠C=90°,BC=3,则AC的长为( )
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
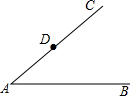 如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)
如图,已知∠CAB及边AC上一点D,在图中求作∠ADE,使得∠ADE与∠CAB是内错角,且∠ADE=∠CAB.(要求:尺规作图,不写作法,保留作图痕迹)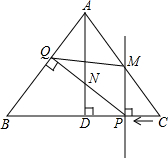 已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题:
已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题: