题目内容
19.某班级劳动时,将全班同学分成n个小组,若每小组10人,则有一组多2人,若每小组12人,则有一组少4人,按下列哪个选项重新分组,能使每组人数相同?( )| A. | 4组 | B. | 5组 | C. | 6组 | D. | 7组 |
分析 根据全班同学人数不变以及“将全班同学分成n个小组,若每小组10人,则有一组多2人;若每小组12人,则有一组少4人”列出方程,求解即可.
解答 解:设将全班同学分成n个小组,根据题意得
10n+2=12n-4,
解得n=3,
所以全班同学共有:10n+2=10×3+2=32人,
32=4×8,
则将全班同学分成4个小组,能使每组人数相同.
故选A.
点评 本题考查了一元一次方程的应用,解题关键是注意抓住题目中的一些关键性词语,找出等量关系,列出方程.

练习册系列答案
相关题目
9. 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
 如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.
如图,在长方形ABCD中无重叠放入面积分别为16cm2和12cm2的两张正方形纸片,则图中空白部分的面积为( )cm2.| A. | 16-8$\sqrt{3}$ | B. | -12+8$\sqrt{3}$ | C. | 8-4$\sqrt{3}$ | D. | 4-2$\sqrt{3}$ |
 将一副三角尺按如图方式进行摆放,则∠1的度数为120°.
将一副三角尺按如图方式进行摆放,则∠1的度数为120°.
 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.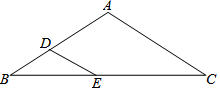 已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点.
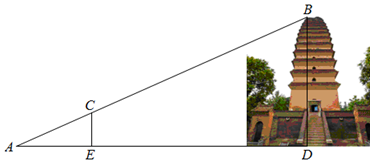
已知等腰△ABC中,AB=AC=5a,BC=8a.点D、E为边AB、BC上两点. 海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号)
海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只,并测得它正以60km/h的速度向北偏东60°的方向航行,缉私艇随即以90km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?(结果保留根号)