Question

11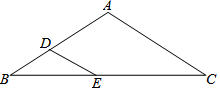．已知等腰△ABC中，AB=AC=5a，BC=8a．点D、E为边AB、BC上两点．
（1）若BD=$\frac{1}{2}$AD，BE=$\frac{1}{2}$CE，求DE的长（用a的代数式表示）；
（2）若BD=2a，当△DBE中有一个角等于$\frac{1}{2}$∠BAC，求此时DE的长（用a的代数式表示）．

Answer 1

分析 （1）证明△BDE∽△BAC，列比例式可求DE的长；
（2）作辅助线，构建直角三角形，根据等腰三角形三线合一的性质得：∠BAG=∠CAG=$\frac{1}{2}$∠BAC，并根据勾股定理求AG的长，当△DBE中有一个角等于$\frac{1}{2}$∠BAC时，分两种情况：①如图1，当∠BDE=$\frac{1}{2}$∠BAC时，②如图2，当∠BED=$\frac{1}{2}$∠BAC时，分别证明△BDE∽△BAG，列比例式可求得DE的长．

解答 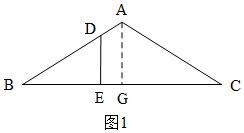解：（1）∵$BD=\frac{1}{2}AD，BE=\frac{1}{2}CE$，
∴$\frac{BD}{AB}=\frac{BE}{BC}=\frac{1}{3}$，
∵∠B=∠B，
∴△BDE∽△BAC，
∴$\frac{DE}{5a}=\frac{1}{3}$，
∴DE=$\frac{5}{3}a$；
（2）过A作AG⊥BC于G，
∴BG=$\frac{1}{2}BC=4a$，
由勾股定理得：AG=3a，
分两种情况：
①如图1，当∠BDE=$\frac{1}{2}$∠BAC时，∠BDE=∠BAG，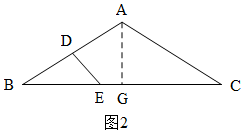
∵∠B=∠B，
∴△BDE∽△BAG，
∴$\frac{2a}{5a}=\frac{DE}{3a}$，
∴DE=$\frac{6}{5}a$；
②如图2，当∠BED=$\frac{1}{2}$∠BAC时，∠BED=∠BAG，
∵∠B=∠B，
∴△BED∽△BAG，
∴$\frac{2a}{4a}=\frac{DE}{3a}$，
∴DE=$\frac{3}{2}a$．
综上所述，DE的长为$\frac{6}{5}$a或$\frac{3}{2}$a．

点评 本题考查了三角形相似的性质和判定、等腰三角形的性质，熟练掌握三角形相似的性质和判定是关键，注意两三角形相似时对应边的比成比例．