题目内容
8．
海关缉私人员驾艇在C处发现正北方向30km的A处有一艘可疑船只，并测得它正以60km/h的速度向北偏东60°的方向航行，缉私艇随即以90km/h的速度在B处将可疑船只拦截．缉私艇从C处到B处需航行多长时间？（结果保留根号）
分析 过B作BD⊥AC于点D，设缉私艇从C处到B处需航行xkm，在直角△ABD中利用三角函数表示出BD和AD，然后在直角△BCD中利用勾股定理即可列方程求解．
解答 
解：设缉私艇从C处到B处需航行xkm，则
AB=60xkm，BC=90xkm．
过B作BD⊥AC于点D，则
AD=30xkm，BD=30$\sqrt{3}$xkm．
根据题意得（90x）2=（30+30x）2+（30$\sqrt{3}$x）2，
即5x2-2x-1=0，
解得x1=$\frac{\sqrt{6}+1}{5}$，x2=$\frac{1-\sqrt{6}}{5}$（舍去）．
答：缉私艇从C处到B处需航行$\frac{1+\sqrt{6}}{5}$小时．
点评 本题考查了解直角三角形，解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．
练习册系列答案
相关题目
环岛是为了减少车辆行驶冲突，在多个交通路口交汇的地方设置的交通设施，多为圆形，它使车辆按统一方向行驶，将冲突点转变为通行点，能有效地减少交通事故的发生，如图是该交通环岛的简化模型（因路段FG施工，禁止从路段EF行驶过来的车辆在环岛内通行，只能往环岛外行驶），某时段内该交通环岛的进出机动车辆数如图所示，图中箭头方向表示车辆的行驶方向．
16．如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠，使AB落在AD边上，折痕为AE，再将△AEB以BE为折痕向右折叠，AE与DC交于点F，则FC：CD的值是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | 1 |
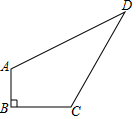如图所示，已知四边形ABCD中，AB=3，BC=4，CD=12，DA=13，且AB⊥BC．求四边形ABCD的面积36．