题目内容
4. 如图,已知圆O,弦AB、CD相交于点M.
如图,已知圆O,弦AB、CD相交于点M.(1)求证:AM•MB=CM•MD;
(2)若M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.
分析 (1)连接AD、BC,利用同弧所对的圆周角相等,证明△ADM∽△CBM;
(2)连接OM、OC,由于M是CD的中点,由垂径定理得OM⊥CD,利用勾股定理可求出CM的值,根据(1)的结论,求出AM•BM.
解答 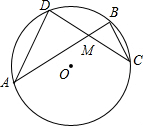 解:(1)连接AD、BC.
解:(1)连接AD、BC.
∵∠A=∠C,∠D=∠B,
∴△ADM∽△CBM
∴$\frac{AM}{CM}=\frac{DM}{BM}$
即AM•MB=CM•MD.
(2)连接OM、OC.
∵M为CD中点,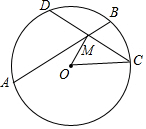
∴OM⊥CD
在Rt△OMC中,∵OC=3,OM=2
∴CD=CM=$\sqrt{O{C}^{2}-O{M}^{2}}$
=$\sqrt{{3}^{2}-{2}^{2}}$
=$\sqrt{5}$
由(1)知AM•MB=CM•MD.
∴AM•MB=$\sqrt{5}$•$\sqrt{5}$
=5.
点评 本题考查了相似三角形的判定和性质、勾股定理、圆周角定理及垂径定理,是综合性较强的题目.(1)利用相似、圆周角定理得到相交弦定理;(2)中利用垂径定理、勾股定理和相交弦定理得到了AM与BM的积.相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等

练习册系列答案
相关题目
15. 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
 如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.
如图,已知钝角△ABC,依下列步骤尺规作图,并保留作图痕迹.步骤1:以C为圆心,CA为半径画弧①;
步骤2:以B为圆心,BA为半径画弧②,交弧①于点D;
步骤3:连接AD,交BC延长线于点H.
下列叙述正确的是( )
| A. | BH垂直平分线段AD | B. | AC平分∠BAD | ||
| C. | S△ABC=BC•AH | D. | BC=CH |
12.下列方程中,没有实数根的是( )
| A. | x2-6x+9=0 | B. | x2-2x+3=0 | C. | x2-x=0 | D. | (x+2)(x-1)=0 |
16.如图,有一矩形纸片ABCD,AB=6,AD=8,将纸片折叠,使AB落在AD边上,折痕为AE,再将△AEB以BE为折痕向右折叠,AE与DC交于点F,则FC:CD的值是( )


| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
14. 如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )
如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )
 如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )
如图,已知直线AB,CD相交于点O,OA平分∠COE,∠EOC=100°,则∠BOD的度数是( )| A. | 50° | B. | 80° | C. | 40° | D. | 100° |
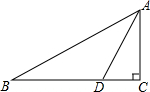 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DC=1,BD=2.求∠B的度数和AC的长.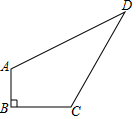 如图所示,已知四边形ABCD中,AB=3,BC=4,CD=12,DA=13,且AB⊥BC.求四边形ABCD的面积36.
如图所示,已知四边形ABCD中,AB=3,BC=4,CD=12,DA=13,且AB⊥BC.求四边形ABCD的面积36.