题目内容
1.若a,b为实数,且|a+1|+$\sqrt{b-1}$=0,则(ab)2014的值为1.分析 根据非负数是性质,两个非负数相加为O,这两个非负数都为0,再代入计算即可.
解答 解:∵|a+1|+$\sqrt{b-1}$=0,
又∵|a+1|≥0,$\sqrt{b-1}$≥0,
∴a+1=0,b-1=0,
∴a=-1,b=1,ab=-1,
∴(ab)2014=(-1)2014=1.
故答案为1.
点评 本题考查非负数的性质、绝对值、二次根式的意义等知识,解题的关键是理解非负数的性质,记住负数的偶次方为正数,属于中考基础题,常考题型.

练习册系列答案
相关题目
10.若方程组$\left\{\begin{array}{l}{ax+by=1}\\{x+2by=-3c}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,则a+b+c=( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{2}{3}$ | D. | -2 |
11.下列线段不能构成直角三角形的是( )
| A. | a=6,b=8,c=10 | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{3}$ | C. | a=3,b=4,c=5 | D. | a=2,b=3,c=$\sqrt{6}$ |

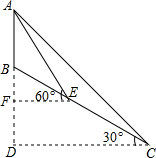 如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.
如图,山顶上有一信号塔AB,山坡BC的坡度为i=1:$\sqrt{3}$,现在为了测量塔高AB,测量人员选择山脚C处为一侧量点,测得塔顶仰角为45°,然后顺山坡向上行走100米到达E处,再测得塔顶仰角为60°,求塔高AB.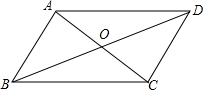 如图,?ABCD的对角线AC,BD相交于点O,△ABO的周长为23cm,AD比CD长2cm,AC与BD的和为34cm,求?ABCD的周长.
如图,?ABCD的对角线AC,BD相交于点O,△ABO的周长为23cm,AD比CD长2cm,AC与BD的和为34cm,求?ABCD的周长. 如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.
如图,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM、ON交于A、B两点,如果∠APB绕点P旋转时始终满足OA•OB=OP2,且∠MON=60°.