题目内容
13.在△ABC中,AB=AC,∠BAC=90°,点D为射线CB上一点,连接AD,以AD为一边在AD右侧作正方形ADEF,连接CF,则∠ACF的大小为45°或135°.分析 ①如图1中,当点D在BC边上时,利用全等三角形的性质推出∠ACF=∠B=45°,②如图2中,当点D在CB的延长线上时,同理可证△ABD≌△ACF推出∠ACF=∠ABD,由此解决问题.
解答  解:①如图1中,当点D在BC边上时,
解:①如图1中,当点D在BC边上时,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=90°,AB=AC
∴∠BAC=∠DAF,∠B=∠ACB=45°,
∴∠BAD=∠CAF,
在△ABD和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△BAD≌△CAF,
∠ACF=∠B=45°.
②如图2中,当点D在CB的延长线上时,同理可证△ABD≌△ACF,
∴∠ACF=∠ABD=180°-45°=135°,
综上所述∠ACF=45°或135°.
故答案为45°或135°.
点评 本题考查正方形的性质、全等三角形的判定和性质,解题的关键是熟练掌握全等三角形的判定和性质,注意有两个解,属于基础题,中考考查图形.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
18.下列运算正确的是( )
| A. | x5•x=x5 | B. | x5-x2=x3 | C. | (-y)2 (-y)7=y9 | D. | -y3•(-y)7=y10 |
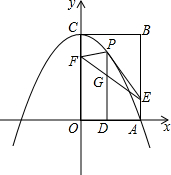 如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PD⊥OA于点D,点E(8,2),F(0,6),连接PE、PF、EF.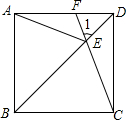 如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE.
如图,在正方形ABCD中,E是对角线BD上任意一点(BE>DE),CE的延长线交AD于点F,连接AE. 如图梯形ABCD中,AD∥BC,F为AD的中点,连接BF并延长与CD的延长线交于点E,且∠ABE=∠ACE.
如图梯形ABCD中,AD∥BC,F为AD的中点,连接BF并延长与CD的延长线交于点E,且∠ABE=∠ACE.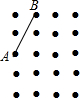 如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.
如图,在4×5的点阵图中,每两个横向和纵向相邻阵点的距离均为1,该点阵图中已有两个阵点分别标为A、B,请在此点阵图中找一个阵点C,使得以点A、B、C为顶点的三角形是等腰三角形,则符合条件的点C有5个.