题目内容
10．若方程组$\left\{\begin{array}{l}{ax+by=1}\\{x+2by=-3c}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$，则a+b+c=（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | -$\frac{2}{3}$ | D． | -2 |
分析 把x与y的值代入方程组求出a，b，c的值，即可求出a+b+c的值．
解答 解：把$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$代入方程组得：$\left\{\begin{array}{l}{3a+b=1}\\{3+2b=-3c}\end{array}\right.$，
整理得：$\left\{\begin{array}{l}{3a+b=1①}\\{2b+3c=-3②}\end{array}\right.$，
①+②得：3a+3b+3c=-2，
则a+b+c=-$\frac{2}{3}$，
故选C．
点评 此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程都成立的未知数的值．
练习册系列答案
相关题目
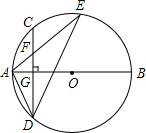如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足$\frac{CF}{FD}$=$\frac{1}{3}$，连接AF并延长交⊙O于点E，连接AD、DE，若CF=2，AF=3，给出下列结论：
18．下列运算正确的是（ ）
| A． | x5•x=x5 | B． | x5-x2=x3 | C． | （-y）2 （-y）7=y9 | D． | -y3•（-y）7=y10 |
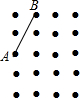如图，在4×5的点阵图中，每两个横向和纵向相邻阵点的距离均为1，该点阵图中已有两个阵点分别标为A、B，请在此点阵图中找一个阵点C，使得以点A、B、C为顶点的三角形是等腰三角形，则符合条件的点C有5个．
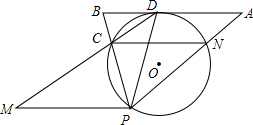如图，在⊙O中，弧DC=弧DN，点P为⊙O上一点，过D作CN的平行线交PN，PC的延长线于A，B，过P作PM∥AB交DC的延长线于M．
20．下列二次根式中，是最简二次根式为（ ）
| A． | $\sqrt{27}$ | B． | $\sqrt{\frac{1}{3}}$ | C． | $\sqrt{{x^2}+{y^2}}$ | D． | $\sqrt{0.3x}$ |