题目内容
13.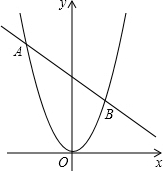 如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点.
如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点.(1)直线AB总经过一个定点C,请直接写出点C坐标;
(2)当k=-$\frac{1}{2}$时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5.
分析 (1)将直线AB的解析式变形为y=k(x+2)+4,由此即可得出直线AB总经过定点C(-2,4);
(2)过点P作PD∥y轴交直线AB于点D,将k=-$\frac{1}{2}$代入直线AB解析式中,联立直线AB与抛物线的解析式成方程组,解之即可得出点A、B的坐标,设点P的坐标为(m,$\frac{1}{2}$m2)(-3<m<2),则点D的坐标为(m,-$\frac{1}{2}$m+3),根据三角形的面积公式结合△ABP的面积等于5即可得出关于m的一元二次方程,解方程即可得出m的值,再将其代入点P的坐标中即可得出结论.
解答 解:(1)∵直线AB的解析式为:y=kx+2k+4=k(x+2)+4,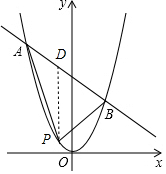
∴直线AB总经过一个定点C,点C的坐标为(-2,4).
(2)过点P作PD∥y轴交直线AB于点D,如图所示.
当k=-$\frac{1}{2}$时,直线AB的解析式为y=-$\frac{1}{2}$x+3,
联立直线AB与抛物线解析式成方程组,得:
$\left\{\begin{array}{l}{y=-\frac{1}{2}x+3}\\{y=\frac{1}{2}{x}^{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=\frac{9}{2}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=2}\\{{y}_{2}=2}\end{array}\right.$,
∴点A的坐标为(-3,$\frac{9}{2}$),点B的坐标为(2,2).
设点P的坐标为(m,$\frac{1}{2}$m2)(-3<m<2),则点D的坐标为(m,-$\frac{1}{2}$m+3),
∴S△ABP=$\frac{1}{2}$PD•(xB-xA)=$\frac{1}{2}$×(-$\frac{1}{2}$m+3-$\frac{1}{2}$m2)×[2-(-3)]=$\frac{5}{2}$×(-$\frac{1}{2}$m2-$\frac{1}{2}$m+3)=5,
解得:m1=-2,m2=1,
∴点P的坐标为(-2,2)或(1,$\frac{1}{2}$).
点评 本题考查了二次函数图象上点的坐标特征以及一次函数图象上点的坐标特征,联立一次函数与二次函数解析式成方程组求出交点坐标是解题的关键.

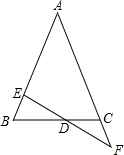 如图,△ABC中,DE=DF,BE=CF,求证:AB=AC.
如图,△ABC中,DE=DF,BE=CF,求证:AB=AC.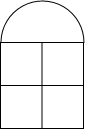 如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)
如图,是一扇窗户的设计图,它由四个小正方形及一个半圆组成,已知半圆的半径为a米.(结果保留π)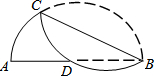 如图将弧BC沿想BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是$\sqrt{114}$.
如图将弧BC沿想BC折叠交直径AB于点D,若AD=5,DB=7,则BC的长是$\sqrt{114}$.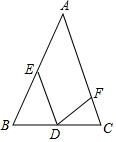 已知:如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF.
已知:如图,在△ABC中,AB=AC,∠EDF=∠B.求证:△BED∽△CDF. 如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.