题目内容
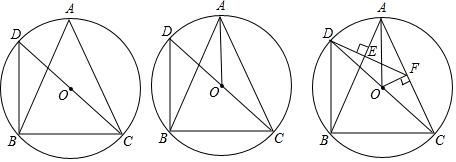
1.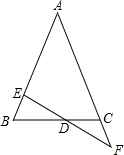 如图,△ABC中,DE=DF,BE=CF,求证:AB=AC.
如图,△ABC中,DE=DF,BE=CF,求证:AB=AC.
分析 作EG∥AC得∠EGB=∠ACB、∠GED=∠F,再证△DEG≌△DFC得CF=GE,结合BE=CF知BE=GE,即可得∠B=∠EGB=∠ACB,从而证得AB=AC.
解答 解:如图,作EG∥AC,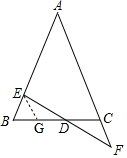
∴∠EGB=∠ACB,∠GED=∠F,
在△DEG和△DFC中,
∵$\left\{\begin{array}{l}{∠GED=∠F}\\{DE=DF}\\{∠EDG=∠FDC}\end{array}\right.$,
∴△DEG≌△DFC(SAS),
∴CF=GE,
又∵BE=CF,
∴BE=GE,
∴∠B=∠EGB,
∴∠B=∠ACB,
∴AB=AC.
点评 本题主要考查全等三角形的判定与性质及等腰三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
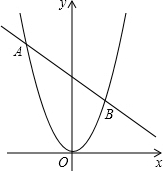 如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点.
如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点. 如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.
如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.