题目内容
2. 如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.
如图,平行四边形ABCD中,点E为DC上一点,连接AE,F为AE上一点,连接BF,∠AFB=∠EFB,G在BF上,连接AG、EG,FG平分∠AGE.(1)求证:AF=EF;
(2)若AG=CE,BG=BC,求证:∠ABF=$\frac{1}{3}$∠AGF.
分析 (1)根据题意推知△EAG为等腰三角形,结合等腰三角形“三线合一”的性质证得结论;
(2)如图,连接EB.构建全等三角形△BGE≌△BCE(SSS),结合全等三角形的对应角相等和平行四边形的对边相互平行的性质推知∠ECB=∠ABE=∠GAB=2∠ABF,∠AGF=∠ABF+∠GAB,
所以∠AGF=3∠ABF,即:∠ABF=$\frac{1}{3}$∠AGF.
解答 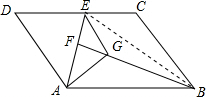 (1)证明:∵∠AFB=∠EFB,
(1)证明:∵∠AFB=∠EFB,
∴∠AFB=∠EFB=90°,即FG⊥AE.
又∵FG平分∠AGE,
∴AF=EF;
(2)解:如图,连接EB.
由(1)知,FG⊥AE,
又∵AF=EF,
∴BE=AB.
∵AG=EC=EG,
∴在△BGE与△BCE中,$\left\{\begin{array}{l}{EG=EC}\\{BG=BC}\\{BE=BE}\end{array}\right.$,
∴△BGE≌△BCE(SSS),
∴∠BEG=∠BEC.
又∵EC∥AB,
∴∠ECB=∠ABE=∠GAB=2∠ABF,∠AGF=∠ABF+∠GAB,
∴∠AGF=3∠ABF,即:∠ABF=$\frac{1}{3}$∠AGF.
点评 本题考查了全等三角形的判定与性质,平行四边形的性质以及等腰三角形的判定与性质.注意题中辅助线的作法是解题的难点.

练习册系列答案
相关题目
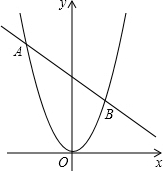 如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点.
如图,已知直线AB:y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点. 如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.
如图.延长线段AB到C,使BC=$\frac{2}{3}$AC.点C是线段BD的中点.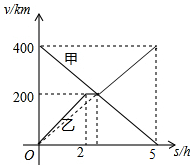 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车距B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车距B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
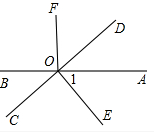 如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.
如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠BOC、∠BOF的度数.