题目内容
6.甲、乙两种水稻试验田连续5年的平均单位面积产量如下:(单位:吨/公顷)| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5 年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
(2)哪种水稻的产量比较稳定.
分析 首先求得平均产量,然后求得方差,比较方差,越小越稳定.
解答 解:(1)$\overline{{x}_{甲}}=\frac{1}{5}(9.8+9.9+10.1+10+10.2)=10$,
$\overline{{x}_{乙}}=\frac{1}{5}(9.4+10.3+10.8+9.7+9.8)=10$,
所以甲、乙两种水稻的平均产量一样高;
(2)甲中水稻产量的方差是:
$\frac{1}{5}$[(9.8-10)2+(9.9-10)2+(10.1-10)2+(10-10)2+(10.2-10)2]=0.02,
乙种水稻产量的方差是:
$\frac{1}{5}$[(9.4-10)2+(10.3-10)2+(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244.
∴0.02<0.244,
∴产量比较稳定的水稻品种是甲.
点评 此题考查了方差,用到的知识点是方差和平均数的计算公式,它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
14.下列计算中,正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
1.下列各组长度中,能构成直角三角形的是( )
| A. | 1,2,3 | B. | $\sqrt{2}$,$\sqrt{3}$,5 | C. | 5,6,7 | D. | 0.3,0.4,0.5 |
11.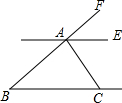 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
 如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )
如图,已知AE∥BC,AC⊥AB,若∠ACB=50°,则∠FAE的度数是( )| A. | 50° | B. | 60° | C. | 40° | D. | 30° |

 如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2).
如图,三角形ABC三个顶点的坐标分别为A(4,3),B(3,1),C(1,2). 如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).
如图,直线y=kx+b与坐标轴相交于点M(3,0),N(0,4).