题目内容
11．
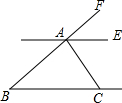如图，已知AE∥BC，AC⊥AB，若∠ACB=50°，则∠FAE的度数是（ ）| A． | 50° | B． | 60° | C． | 40° | D． | 30° |
分析 由AE∥BC，∠ACB=50°，根据两直线平行，内错角相等，即可求得∠EAC的度数，又由AC⊥AB，求得答案．
解答 解：∵AE∥BC，∠ACB=50°，
∴∠EAC=∠ACB=50°，
∵AC⊥AB，
∴∠FAC=90°，
∴∠FAE=90°-∠EAC=40°．
故选C．
点评 此题考查了平行线的性质以及垂线的性质．注意掌握两直线平行，内错角相等定理的应用是解此题的关键．
练习册系列答案
能考试全能100分系列答案
相关题目
2．
如图，线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心，AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是（ ）
如图，线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心，AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是（ ）| A． | 1+$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\sqrt{2}-1$ | D． | 1 |
先阅读理解下面的例题，再按要求解答下列问题：
6．甲、乙两种水稻试验田连续5年的平均单位面积产量如下：（单位：吨/公顷）
（1）哪种水稻的平均单位面积产量比较高？
（2）哪种水稻的产量比较稳定．
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5 年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
（2）哪种水稻的产量比较稳定．
如图，在平面直角坐标系中，点A的坐标为（-2，2），点B与点A关于x轴对称，点B先向右平移4个单位长度，再向上平移2个单位长度得到点C．