题目内容
5. 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.若CG=8,则S四边形BCDG=16$\sqrt{3}$.
分析 先根据在菱形ABCD中,AB=BD判断出△ABD为等边三角形,故可得出∠A的度数,再由菱形的性质求出∠BCD的度数,由三角形外角的性质得出点B、C、D、G四点共圆,过点C作CM⊥GB于M,CN⊥GD于N,根据HL定理得出△CBM≌△CDN,由四边形BCDG=S四边形CMGN,S四边形CMGN=2S△CMG即可得出结论.
解答 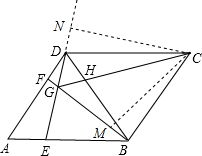 解:∵四边形ABCD为菱形,
解:∵四边形ABCD为菱形,
∴AB=AD.
∵AB=BD,
∴△ABD为等边三角形.
∴∠A=∠BDF=60°.
∴∠BCD=60°,
∵∠BGE=∠BDG+∠DBF=∠BDG+∠GDF=60°=∠BCD,即∠BGD+∠BCD=180°,
∴点B、C、D、G四点共圆,
∴∠BGC=∠BDC=60°,∠DGC=∠DBC=60°.
∴∠BGC=∠DGC=60°.
过点C作CM⊥GB于M,CN⊥GD于N.
∴CM=CN,
在Rt△CBM与Rt△CDN中,
$\left\{\begin{array}{l}{CM=CN}\\{BC=CD}\end{array}\right.$,
∴△CBM≌△CDN(HL),
∴S四边形BCDG=S四边形CMGN.S四边形CMGN=2S△CMG,
∵∠CGM=60°,
∴GM=$\frac{1}{2}$CG,CM=$\frac{\sqrt{3}}{2}$CG,
∴S四边形BCDG=S四边形CMGN=2S△CMG=2×$\frac{1}{2}$×$\frac{1}{2}$CG×$\frac{\sqrt{3}}{2}$CG=$\frac{\sqrt{3}}{4}$CG2=$\frac{\sqrt{3}}{4}$×82=16$\sqrt{3}$.
故答案为:16$\sqrt{3}$.
点评 此题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质以及圆的内接四边形的性质.注意准确作出辅助线是解此题的关键.

(1)填表:
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
(3)证明你的猜想.
| A. | $\sqrt{8a}$ | B. | $\sqrt{5a}$ | C. | $\sqrt{0.5x}$ | D. | $\sqrt{{a}^{2}+{a}^{2}b}$ |
 小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题:
小明每天早上步行到学校上学.一天,小明从家里出发后5分钟时,他爸爸发现他忘了带语文书,于是,爸爸立即以180米/分的速度沿相同路线去追小明,并在途中追上小明,设小明离开家的时间为x(分),如图图象中的线段OA表示小明从家到学校的过程中离开家的距离y1(米)与x(分)的关系;线段BP表示爸爸追赶小明时离开家的距离y2(米)与x(分)之间的关系,请分析图中的信息并解答下列问题: