题目内容
16.如果$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1,那么$\frac{ab}{|ab|}$+$\frac{bc}{|bc|}$+$\frac{ac}{|ac|}$+$\frac{abc}{|abc|}$的值为( )| A. | -2 | B. | -1 | C. | 0 | D. | 不确定 |
分析 根据$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1,可得a、b、c有两个是负数,一个是正数,根据有理数的除法,可得答案.
解答 解:∵$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1,
∴a、b、c有两个是负数,一个是正数,
假设a>0,b<0,c<0,
则$\frac{ab}{|ab|}$+$\frac{bc}{|bc|}$+$\frac{ac}{|ac|}$+$\frac{abc}{|abc|}$=-1+1-1+1=0.
故选:C.
点评 本题考查了有理数的除法,利用$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=-1得出a、b、c有两个是负数,一个是正数是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知关于x,y的方程中$\left\{\begin{array}{l}{3x+4y=7}\\{5x-4y=m}\end{array}\right.$的解互为相反数,则m的值为( )
| A. | 63 | B. | 7 | C. | -63 | D. | -7 |
5.若3x=a,3y=b,则32x+y的值为( )
| A. | a2b | B. | ab2 | C. | ab | D. | 3a2b |
6.下列式子中,正确的是( )
| A. | $\sqrt{(±3)^{2}}$=±3 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{{3}^{2}}$=±3 | D. | -$\sqrt{{3}^{2}}$=-3 |
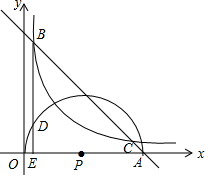 如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
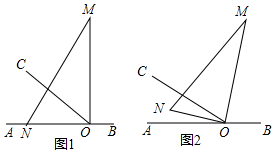
如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D. 如图,直线EF分别与直线AB、CD相交于点M、N,且∠1=∠2,MO、NO分别平分∠BMF和∠END,试判断△MON的形状,并说明理由.
如图,直线EF分别与直线AB、CD相交于点M、N,且∠1=∠2,MO、NO分别平分∠BMF和∠END,试判断△MON的形状,并说明理由.