题目内容
2.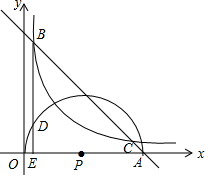 如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.
如图,已知y=-x+m(m>4)过动点A(m,0),并与反比例函数y=$\frac{4}{x}$的图象交于B、C两点(点B在点C的左边),以OA为直径作反比例函数y=$\frac{4}{x}$的图象相交的半圆,圆心为P,过点B作x轴的垂线,垂足为E,并于半圆P交于点D.(1)当m=5时,求B、C两点的坐标.
(2)求证:无论m取何值,线段DE的长始终为定值.
(3)记点C关于直线DE的对称点为C′,当四边形CDC′E为菱形时,求m的值.
分析 (1)把M=5代入一次函数解析式中,与反比例函数列方程组解出即可;
(2)作辅助线,如图1,证明△ODE∽△DAE,列比例式得:$\frac{DE}{AE}=\frac{OE}{DE}$,则DE2=OE•AE=OE•BE=4,所以线段DE的长始终为定值;
(3)根据菱形的性质求出C的坐标,代入一次函数的解析式中可得m的值.
解答 解:(1)把m=5代入y=-x+m中得:y=-x+5,
则$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{4}{x}}\end{array}\right.$ 解得:$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=4}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=1}\end{array}\right.$,
∴B(1,4),C(4,1);
(2)如图1,连接OD、AD,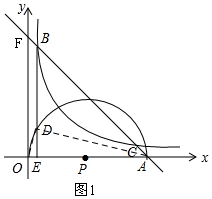
∵A(m,0),
∴OA=m,
y=-x+m中,当x=0时,y=m,则F(0,m),
∴OF=m,
∴△AOF是等腰直角三角形,
∴∠OAB=45°,
∵BE⊥OA,
∴△ABE是等腰直角三角形,
∴BE=AE,
∵OA是⊙P的直径,
∴∠ODA=90°,
∵∠ODE=∠OAD,
∵∠OED=∠DEA=90°,
∴△ODE∽△DAE,
∴$\frac{DE}{AE}=\frac{OE}{DE}$,
∴DE2=OE•AE=OE•BE,
∵B是反比例函数上的点,即OE•BE=4
∴无论m取何值,线段DE的长始终为定值;
(3)如图3,连接CC′,设DE与CC′交于G,
由(2)得:DE2=4,
∴DE=2,
∵四边形CDC′E为菱形,
∴DG=EG=1,
∴C的纵坐标为1,
当y=1时,$\frac{4}{x}$=1,x=4,
∴C(4,1),
把C(4,1)代入y=-x+m中得:-4+m=1,
m=5.
点评 本题是圆与函数的综合题,考查了利用待定系数法求一次函数的解析式、利用方程组的解求两函数的交点坐标、菱形的性质、三角形相似的性质和判定等知识,涉及的知识点较多,比较复杂,熟练掌握三角形相似的判定及菱形的性质是关键.

 如图,数轴上点A,B所表示的数分别是4,8.
如图,数轴上点A,B所表示的数分别是4,8.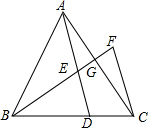 如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.
如图,已知△ABC中,D、G分别是边BC、AC上的点,连AD、BC相交于点E,BE=BD.过点C作AD的平行线与BG的延长线于点F,$\frac{CD}{BD}$=$\frac{1}{2}$,$\frac{DE}{EA}$=$\frac{2}{3}$.