据题设条件作出所研究问题的曲线或有关图形,借助几何图形的直观性作出正确判断的方法叫图解法或数形结合法。
[例10](97年高考题)椭图C与椭圆 +
+ =1关于直线x+y=0对称,椭圆C的方程是_____。
=1关于直线x+y=0对称,椭圆C的方程是_____。
A. +
+ =1 B.
=1 B.  +
+ =1
=1
C.  +
+ =1 D.
=1 D.  +
+ =1
=1
[解]图解法:作出椭圆及对称的椭圆C,由中心及焦点位置,容易得到选A。
[另解]直接法:设椭圆C上动点(x,y),则对称点(-y,-x),代入已知椭圆方程得 +
+ =1,整理即得所求曲线C方程,所以选A。
=1,整理即得所求曲线C方程,所以选A。
[例11](87年高考题)在圆x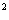 +y
+y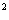 =4上与直线4x+3y-12=0距离最小的点的坐标是_____。
=4上与直线4x+3y-12=0距离最小的点的坐标是_____。
|
y
O
x |
A. ( ,
, ) B. (
) B. ( ,-
,- ) C. (-
) C. (- ,
, )
D. (-
)
D. (- ,-
,- )
)
 [解]图解法:在同一直角坐标系中作出圆x
[解]图解法:在同一直角坐标系中作出圆x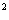 +y
+y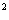 =4和直线4x+3y-12=0后,由图可知距离最小的点在第一象限内,所以选A。
=4和直线4x+3y-12=0后,由图可知距离最小的点在第一象限内,所以选A。
[直接法]先求得过原点的垂线,再与已知直线相交而得。
 M - i
2
M - i
2    |
[例12]已知复数z的模为2,则 |z-i| 的最大值为_______。
A. 1 B. 2 C.  D. 3
D. 3
[解]图解法:由复数模的几何意义,画出右图,可知当圆上的点到M的距离最大时即为|z-i|最大。所以选D;
[另解]不等式法或代数法或三角法:
|z-i|≤|z|+|i|=3,所以选D。
数形结合,借助几何图形的直观性,迅速作正确的判断是高考考查的重点之一;97年高考选择题直接与图形有关或可以用数形结合思想求解的题目约占50%左右。
从考试的角度来看,解选择题只要选对就行,不管是什么方法,甚至可以猜测。但平时做题时要尽量弄清每一个选择支正确理由与错误的原因,这样,才会在高考时充分利用题目自身的提供的信息,化常规为特殊,避免小题作,真正做到熟练、准确、快速、顺利完成三个层次的目标任务。
Ⅱ、巩固性题组:
1.(86年高考题)函数y=( )
) +1的反函数是______。
+1的反函数是______。
A. y=log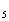 x+1 (x>0)
B. y=log
x+1 (x>0)
B. y=log 5+1 (x>0且x≠1)
5+1 (x>0且x≠1)
C. y=log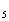 (x-1) (x>1) D. y=log
(x-1) (x>1) D. y=log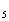 x-1 (x>1)
x-1 (x>1)
一些计算过程复杂的代数、三角、解析几何问题,可以作出有关函数的图像或者构造适当的几何图形,利用图示辅助进行直观分析,从而得出结论。这也就是数形结合的解题方法。
    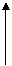  y y
 O 2 x
O 2 x |
[例5]不等式 >x+1的解集是
。
>x+1的解集是
。
[解]如图,在同一坐标系中画出函数y= 与y=x+1的图像,由图中可以直观地得到:-
与y=x+1的图像,由图中可以直观地得到:- ≤x<2,所以所求解集是[-
≤x<2,所以所求解集是[- ,2)。
,2)。
     y
O 1 3|k| x y
O 1 3|k| x |
[例6](93年高考题)若双曲线 -
- =1与圆x
=1与圆x +y
+y =1没有公共点,则实数k的取值范围是
。
=1没有公共点,则实数k的取值范围是
。
[解]在同一坐标系中作出双曲线 -
- =1与圆x
=1与圆x +y
+y =1,由双曲线的顶点位置的坐标,可以得到|3k|>1,故求得实数k的取值范围是k>
=1,由双曲线的顶点位置的坐标,可以得到|3k|>1,故求得实数k的取值范围是k> 或k<-
或k<- 。
。
 +ax+bx-8,且f(-2)=10,那么f(2)等于_____。
+ax+bx-8,且f(-2)=10,那么f(2)等于_____。 -2x)+sin2x的最小正周期是_____。
-2x)+sin2x的最小正周期是_____。 B.
B.  C. 2
C. 2 cos2x-
cos2x- sin2x+sin2x=sin(2x+
sin2x+sin2x=sin(2x+ ),T=π,选B。
),T=π,选B。 等于_____。
等于_____。 B.
B.
 C.
C.  D.
D.
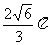
 、
、 、
、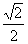 、
、 ,再求得h分别为:
,再求得h分别为: 、
、 πr
πr
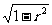 =
=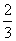 π
π
 ,所以
,所以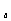 (2-ax)在[0,1]上是x的减函数,则a的取值范围是_____。
(2-ax)在[0,1]上是x的减函数,则a的取值范围是_____。 ,消y得:
,消y得: ,消k得y
,消k得y +C
+C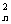 +…+C
+…+C +C
+C =______。
=______。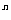 B. 2
B. 2 C. 2
C. 2 D. (n-1)2
D. (n-1)2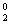 +C
+C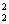 =2,排除答案A、C;当n=4时,代入得C
=2,排除答案A、C;当n=4时,代入得C +C
+C +C
+C =8,排除答案D。所以选B。
=8,排除答案D。所以选B。 ,选B。
,选B。 x>cos
x>cos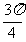 <x<2k
<x<2k ,k
,k Z} B.
{x|2k
Z} B.
{x|2k ,k
,k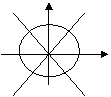
 +2kπ,选D;
+2kπ,选D; 种,其中甲、乙两人相邻的排法有2×P
种,其中甲、乙两人相邻的排法有2×P 种。因此,甲、乙两人必需不相邻的排法种数有:P
种。因此,甲、乙两人必需不相邻的排法种数有:P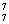 -2×P
-2×P ×P
×P =3600。
=3600。 =a
=a +a
+a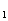 x+a
x+a x
x x
x +4)=
+4)= ,V
,V ,则V
,则V ,θ∈(0,π),则ctgθ的值是 。
,θ∈(0,π),则ctgθ的值是 。 ,解方程组得sinθ=
,解方程组得sinθ= ,cosθ=
,cosθ= ,故答案为:-
,故答案为:- 。
。 =t,再利用万能公式求解。
=t,再利用万能公式求解。 (x+1)=5的解是 。
(x+1)=5的解是 。