摘要：直接从题设条件出发.运用有关概念.性质.定理.法则等知识.通过推理运算.得出结论.再对照选择项.从中选正确答案的方法叫直接法. [例1]若sinx>cosx,则x的取值范围是 . A．{x|2k-<x<2k+,kZ} B. {x|2k+<x<2k+,kZ} C. {x|k-<x<k+,kZ} D. {x|k+<x<k+,kZ} [解]直接解三角不等式:由sinx>cosx得cosx-sinx<0,即cos2x<0.所以: +2kπ<2x<+2kπ.选D, [另解]数形结合法:由已知得|sinx|>|cosx|.画出单位圆: 利用三角函数线.可知选D. [例2]是是的奇函数.f.当0≤x≤1时.f等于 . A. 0.5 B. -0.5 C. 1.5 D. -1.5 [解]由f＝-f＝f是奇函数得f＝-0.5.所以选B. 也可由f.得到周期T＝4.所以f＝-f(0.5)＝-0.5. [例3]七人并排站成一行.如果甲.乙两人必需不相邻.那么不同的排法的种数是 . A. 1440 B. 3600 C. 4320 D. 4800 [解一]用排除法:七人并排站成一行.总的排法有P种.其中甲.乙两人相邻的排法有2×P种.因此.甲.乙两人必需不相邻的排法种数有:P-2×P＝3600,对照后应选B, [解二]用插空法:P×P＝3600. 直接法是解答选择题最常用的基本方法.低档选择题可用此法迅速求解.直接法适用的范围很广.只要运算正确必能得出正确的答案.提高直接法解选择题的能力.准确地把握中档题目的“个性 .用简便方法巧解选择题.是建在扎实掌握“三基 的基础上.否则一味求快则会快中出错.
网址：http://m.1010jiajiao.com/timu_id_4413465[举报]
证明是直接从原命题的条件逐步推得命题成立的，这种证明通常称为________，其一般形式为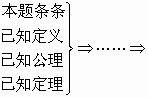
本题结论．其中从已知条件出发，以已知的定义、定理、公理为依据，逐步下推，直到推出要证明的结论为止，这种证明方法称为________，推证过程为
已知条件
…………
结论．而从问题的结论出发，追溯导致结论成立的条件，逐步上溯直到使结论成立的条件和已知条件或已知事实吻合为止，这种证明方法常称为________，推证过程为
……
……．
（2003•北京）设y=f（x）是定义在区间[-1，1]上的函数，且满足条件，①f（-1）=f（1）=0，②对任意的u、v∈[-1，1]，都有|f（u）-f（v）|≤|u-v|
（Ⅰ）证明：对任意x∈[-1，1]，都有x-1≤f（x）≤1-x
（Ⅱ）证明：对任意的u，v∈[-1，1]都有|f（u）-f（v）|≤1
（Ⅲ）在区间[-1，1]上是否存在满足题设条件的奇函数y=f（x）且使得
；若存在请举一例，若不存在，请说明理由．
查看习题详情和答案>>
（Ⅰ）证明：对任意x∈[-1，1]，都有x-1≤f（x）≤1-x
（Ⅱ）证明：对任意的u，v∈[-1，1]都有|f（u）-f（v）|≤1
（Ⅲ）在区间[-1，1]上是否存在满足题设条件的奇函数y=f（x）且使得
|
（2012•福建模拟）对于非空实数集A，记A*={y|?x∈A，y≥x}．设非空实数集合M⊆P，若m＞1时，则m∉P． 现给出以下命题：
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*=∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a+b∈P*；
其中正确的命题是
查看习题详情和答案>>
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*=∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a+b∈P*；
其中正确的命题是
①④
①④
（写出所有正确命题的序号）
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）． 查看习题详情和答案>>
如图，己知|