0 53356 53364 53370 53374 53380 53382 53386 53392 53394 53400 53406 53410 53412 53416 53422 53424 53430 53434 53436 53440 53442 53446 53448 53450 53451 53452 53454 53455 53456 53458 53460 53464 53466 53470 53472 53476 53482 53484 53490 53494 53496 53500 53506 53512 53514 53520 53524 53526 53532 53536 53542 53550 447348
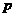 ,
,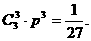 ∴
∴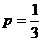
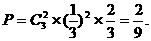 …………………………6分
…………………………6分 的可能取值为0,1,2,
的可能取值为0,1,2,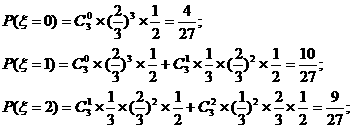
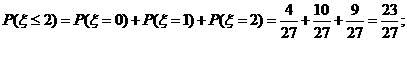
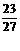 。…………………12分
。…………………12分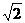 ,
,
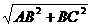 =
=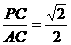 ,
,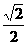 . ……………… 8分
. ……………… 8分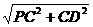 =
=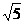 , 又CM⊥PD,
, 又CM⊥PD,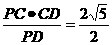
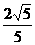 , ∴tan∠CMB=
, ∴tan∠CMB=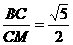 ,
,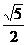 .
……………… 12分
.
……………… 12分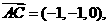
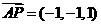 ………………7分
………………7分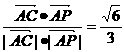 ,
,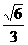 . ………………8分
. ………………8分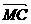 =(-x,-y,-z),
=(-x,-y,-z),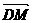 =(x-2,y,z),
=(x-2,y,z),
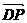 =(-2,0,1),
=(-2,0,1),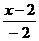 =z, ②
=z, ②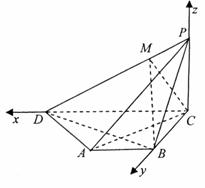
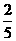 ,y=0,z=
,y=0,z=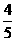 ,
,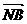 =(-
=(-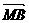 ·
·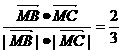 ,
,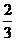 .
………………12分
.
………………12分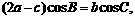
 ………………2分
………………2分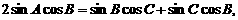
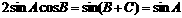 ,
………………4分
,
………………4分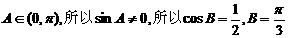 .……………………6分
.……………………6分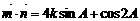 ……………………7分
……………………7分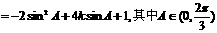 ……………………8分
……………………8分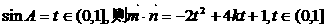 , 又k>1
, 又k>1 取得最大值.
……………………9分
取得最大值.
……………………9分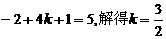 ,符合题意. 所以,
,符合题意. 所以,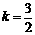 . ………12分
. ………12分 13. 60
13. 60 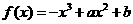 (a,b∈R).
(a,b∈R).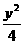 =1,过点M(0,1)的直线l与椭圆C相交于两点A、B.
=1,过点M(0,1)的直线l与椭圆C相交于两点A、B.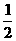 ),求│
),求│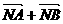 │的最大值.
│的最大值.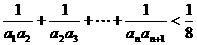 .
.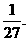
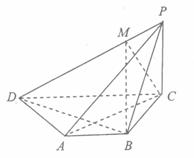
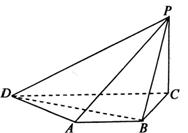 AB∥CD,又AB=BC=PC=1,PB=
AB∥CD,又AB=BC=PC=1,PB=