(15)(本小题13分)
若函数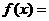
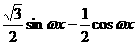 (
(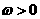 )的最小正周期为
)的最小正周期为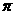 。
。
(I)求 的值;
的值;
(II)求函数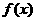 在区间
在区间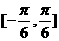 上的取值范围。
上的取值范围。
(16)(本小题共13分)
某车站每天8∶00~9∶00,9∶00~10∶00都恰有一辆客车到站,各车到站时刻是随机的,且各车到站的时间相互独立,其规律为
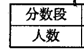
|
到站时刻 |
8∶10 |
8∶30 |
8∶50 |
9∶10 |
9∶30 |
9∶50 |
|
概率 |
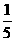 |
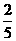 |
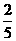 |
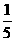 |
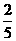 |
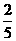 |
一旅客8∶20到车站,求:
(I) 该旅客9点之前乘上车的概率;
(II) 该旅客候车时间超过1小时的概率.
(17)(本小题共14分)
在长方体ABCD-A1B1C1D1中,已知AB=BC=2,BB1=3,连接BC1,过B1作B1E⊥BC1
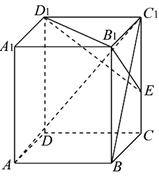 交CC1于点E
交CC1于点E
(I)求证:AC1⊥平面B1D1E;
(II)求二面角E-B1D1-C1的平面角大小
(18)(本小题共13分)
已知函数f(x)=x3+ax2+bx+c在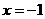 时取得极值,在
时取得极值,在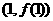 点的切线斜率为4.
点的切线斜率为4.
(I)求a、b的值与函数f(x)的单调区间
(II)若对xÎ[-1,2],不等式f(x)<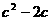 恒成立,求c的取值范围。
恒成立,求c的取值范围。
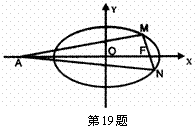
(19)(本小题共14分)
椭圆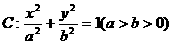 过点P
过点P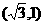 ,且离心率为
,且离心率为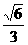 ,
,
F为椭圆的右焦点,过F作直线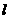 交椭圆C于M、N两点,定点A(
交椭圆C于M、N两点,定点A(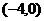 )。
)。
(I)求椭圆C的方程;
 (II)当
(II)当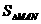 =3
=3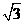 时, 求直线MN的方程.
时, 求直线MN的方程.
(20)(本小题共14分)
已知等差数列{an}前三项为a,4,3a,前n项和为Sn。
(I)求a及{an}的通项公式;
(II)若Sk = 2550,求k的值;
(III)求证:
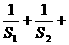 …
…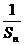 <1.
<1.
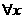 ∈R,cosx≤1,则 ( )
∈R,cosx≤1,则 ( ) p:
p: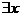 ∈R,cosx
∈R,cosx 1 B.
1 B. P:
P: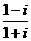 ,则z的共轭复数为 ( )A.-i B.i C.2i D.1+i
,则z的共轭复数为 ( )A.-i B.i C.2i D.1+i 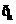 M={5,7},则实数a的值为 ( )
M={5,7},则实数a的值为 ( )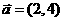 ,
,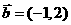 .若
.若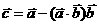 ,则
,则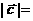 _ 。
_ 。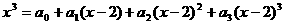 ,则
,则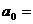 。
。 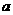 、b、c ,若
、b、c ,若 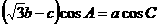 ,则
,则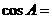 _________________。
_________________。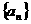 是首项为1公比为3的等比数列,把
是首项为1公比为3的等比数列,把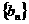 ,则数列
,则数列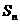 =_____ __。
=_____ __。 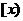 表示超过
表示超过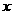 的最小整数,如
的最小整数,如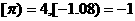 ,则[2)
=___ _。
,则[2)
=___ _。 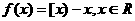 ,则值域为
,则值域为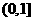 ;
;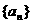 是等差数列,
是等差数列,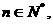 那么数列
那么数列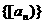 也是等差数列;
也是等差数列;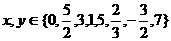 ,则方程
,则方程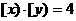 有5组解;
有5组解;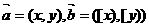 ,则向量a、b的夹角不可能为直角.
,则向量a、b的夹角不可能为直角.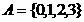 ,
,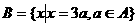 ,则集合
,则集合 等于
等于 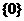 B.
B.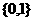 C.
C.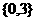
 D.
D.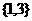
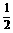 =0对称 D.y轴对称
=0对称 D.y轴对称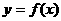 的导函数为
的导函数为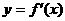 ,那么
,那么 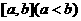 上单调递增的充要条件是
上单调递增的充要条件是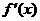 在区间
在区间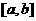 上
上
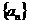 中,已知
中,已知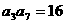 ,则
,则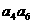 的值为
的值为
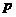 :
: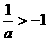 ,
,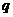 :
: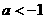 ,则
,则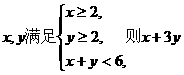 的取值范围是
的取值范围是 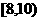 B.[8,10]
B.[8,10] 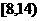
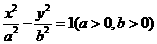 的右焦点为
的右焦点为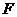 ,若过点
,若过点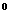 的直线与双曲线渐近线平行,则此双曲线离心率的值为
的直线与双曲线渐近线平行,则此双曲线离心率的值为
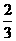 B.2
C.
B.2
C.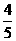 D.3
D.3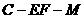 是直二面角,在平面
是直二面角,在平面 中 有两点A,B到棱EF的距离分别为2,4,动点P在平面CF内,若PA,PB与平面CF成的角相等,动点P的轨迹为
中 有两点A,B到棱EF的距离分别为2,4,动点P在平面CF内,若PA,PB与平面CF成的角相等,动点P的轨迹为
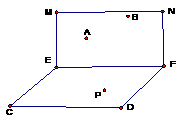 A. 圆 B. 椭圆 C. 双曲线 D.抛物线
A. 圆 B. 椭圆 C. 双曲线 D.抛物线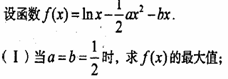
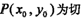


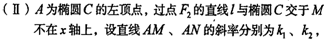
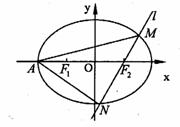
 已知三棱柱ABC-A1B1C1的底面三角形ABC是等腰直角三角形,ÐACB=
已知三棱柱ABC-A1B1C1的底面三角形ABC是等腰直角三角形,ÐACB=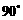 ,点E是AB的中点,点P是棱CC1的中点,如图.
,点E是AB的中点,点P是棱CC1的中点,如图.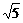 ,求三棱锥P-ABB1的体积.
,求三棱锥P-ABB1的体积.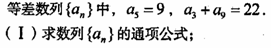
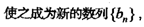
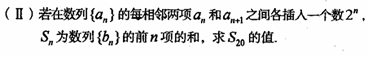
 .
.