0 53357 53365 53371 53375 53381 53383 53387 53393 53395 53401 53407 53411 53413 53417 53423 53425 53431 53435 53437 53441 53443 53447 53449 53451 53452 53453 53455 53456 53457 53459 53461 53465 53467 53471 53473 53477 53483 53485 53491 53495 53497 53501 53507 53513 53515 53521 53525 53527 53533 53537 53543 53551 447348
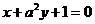 与直线
与直线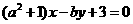 互相垂直,
互相垂直,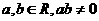 ,则
,则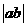 的最小值为
的最小值为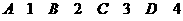
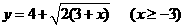 ,则它的反函数为
,则它的反函数为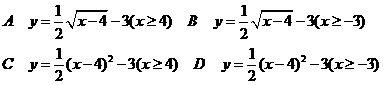
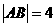 ,动点P满足
,动点P满足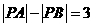 ,则
,则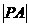 的最小值为
的最小值为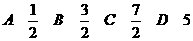
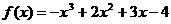 在点(2 , 2)处的切线的倾斜角为
在点(2 , 2)处的切线的倾斜角为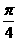 B.
B. 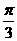 C.
C.
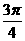 D.
D.
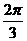
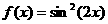 的最小正周期是
的最小正周期是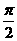 C.
C.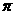 D.
D.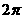
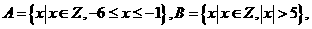 则
则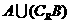 中元素个数为
中元素个数为
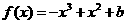 ,
, 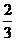 a,
5分
a,
5分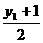 =0,解得y1=-1,
1分
=0,解得y1=-1,
1分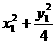 =1,即
=1,即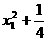 =1,解得x1=±
=1,解得x1=±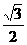 ,
,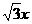 -3y+3=0,或4
-3y+3=0,或4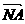 =(x1,y1-
=(x1,y1-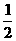 ),
),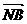 =(x2,y2-
=(x2,y2-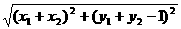 , 8分
, 8分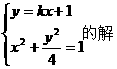 ,
,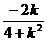 ,
,
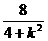 ,
10分
,
10分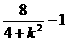 )2=
)2=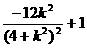 ≤1,
≤1,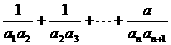
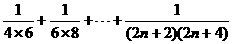 7分
7分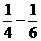 )+
)+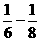 )+…+1
)+…+1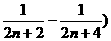 8分
8分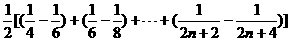
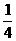
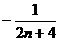 )
)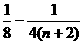 . 10分
. 10分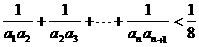 . 12分
. 12分