摘要:3. 已知函数的图象过点.且函数的图象关于y轴对称. (Ⅰ)求m.n的值及函数y=f(x)的单调区间, (Ⅱ)若a>0.求函数y=f(x)在区间(a-1,a+1)内的极值. 解:(1)由函数f(x)图象过点.得m-n=-3, --① 由f(x)=x3+mx2+nx-2.得f′(x)=3x2+2mx+n, 则g(x)=f′(x)+6x=3x2+(2m+6)x+n; 而g(x)图象关于y轴对称.所以-=0.所以m=-3, 代入①得n=0. 于是f′(x)=3x2-6x=3x(x-2). 由f′(x)>得x>2或x<0, 故f(x)的单调递增区间是, 由f′(x)<0得0<x<2, 故f(x)的单调递减区间是(0.2). 得f′(x)=3x(x-2), 令f′(x)=0得x=0或x=2. 当x变化时.f′(x).f(x)的变化情况如下表: X 0 (0,2) 2 f′(x) + 0 - 0 + f(x) 极大值 极小值 由此可得: 当0<a<1时.f(x)在(a-1,a+1)内有极大值f(O)=-2,无极小值, 当a=1时.f(x)在(a-1,a+1)内无极值, 当1<a<3时.f(x)在(a-1,a+1)内有极小值f(2)=-6.无极大值, 当a≥3时.f(x)在(a-1,a+1)内无极值. 综上得:当0<a<1时.f(x)有极大值-2.无极小值.当1<a<3时.f(x)有极小值-6.无极大值,当a=1或a≥3时.f(x)无极值.
网址:http://m.1010jiajiao.com/timu3_id_527687[举报]
 的图象过点
的图象过点 ,且在
,且在 内
内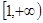 上单调递增.
上单调递增. 的解析式;
的解析式; ,不等式
,不等式 恒成立,试问
恒成立,试问 是否存在.若存在,请求出
是否存在.若存在,请求出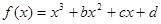 的图象过点P
的图象过点P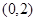 ,
且在点M
,
且在点M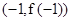 处的切线方程为
处的切线方程为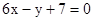 .
.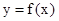 的解析式; (2) 求函数
的解析式; (2) 求函数