摘要:21.解: (Ⅰ)方程可化为. 当时..···································································································· 2分 又. 于是解得 故.········································································································· 6分 (Ⅱ)设为曲线上任一点.由知曲线在点处的切线方程为 . 即. 令得.从而得切线与直线的交点坐标为. 令得.从而得切线与直线的交点坐标为.·············· 10分 所以点处的切线与直线.所围成的三角形面积为 . 故曲线上任一点处的切线与直线.所围成的三角形的面积为定值.此定值为. 12分
网址:http://m.1010jiajiao.com/timu3_id_527689[举报]
设双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点 能否作出直线
能否作出直线 ,使
,使 与双曲线
与双曲线 交于
交于 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
【解析】(1)根据离心率先求出a2的值,然后令双曲线等于右侧的1为0,解此方程可得双曲线的渐近线方程.
(2)设直线l的方程为 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
查看习题详情和答案>>
已知函数 ,
, .
.
(Ⅰ)若函数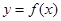 依次在
依次在 处取到极值.求
处取到极值.求 的取值范围;
的取值范围;
(Ⅱ)若存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立.求正整数
恒成立.求正整数 的最大值.
的最大值.
【解析】第一问中利用导数在在 处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
处取到极值点可知导数为零可以解得方程有三个不同的实数根来分析求解。
第二问中,利用存在实数 ,使对任意的
,使对任意的 ,不等式
,不等式
 恒成立转化为
恒成立转化为 ,恒成立,分离参数法求解得到范围。
,恒成立,分离参数法求解得到范围。
解:(1)
①

(2)不等式  ,即
,即 ,即
,即 .
.
转化为存在实数 ,使对任意的
,使对任意的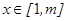 ,不等式
,不等式 恒成立.
恒成立.
即不等式 在
在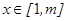 上恒成立.
上恒成立.
即不等式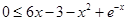 在
在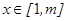 上恒成立.
上恒成立.
设 ,则.
,则.
设 ,则
,则 ,因为
,因为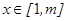 ,有
,有 .
.
故 在区间
在区间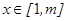 上是减函数。又
上是减函数。又
故存在 ,使得
,使得 .
.
当 时,有
时,有 ,当
,当 时,有
时,有 .
.
从而 在区间
在区间 上递增,在区间
上递增,在区间 上递减.
上递减.
又 [来源:]
[来源:]

所以当 时,恒有
时,恒有 ;当
;当 时,恒有
时,恒有
 ;
;
故使命题成立的正整数m的最大值为5
查看习题详情和答案>>
 :Ax+By+C=0(
:Ax+By+C=0( ),点
),点 在
在



 :Ax+By+C=0(
:Ax+By+C=0( ),点
),点 在
在



 .
. 的值域;
的值域; ,若对
,若对 ,
,
 ,恒
,恒 成立,试求实数
成立,试求实数 的取值范围
的取值范围

 ,则
,则 ,即当
,即当 时,
时, ,又由(Ⅰ)知
,又由(Ⅰ)知

 转化得到。
转化得到。 ,即当
,即当
 ,即
,即 的取值范围是
的取值范围是