13.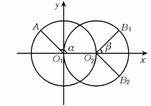 用向量方法证明:半径和圆心距均为1的两个圆⊙O1、⊙O2,在第一个圆的圆周上任取一点A,在第二个圆的圆周上取关于两圆连心线对称的两个点B1、B2.求证:
用向量方法证明:半径和圆心距均为1的两个圆⊙O1、⊙O2,在第一个圆的圆周上任取一点A,在第二个圆的圆周上取关于两圆连心线对称的两个点B1、B2.求证: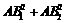 ≥2,并指明等号成立的条件.
≥2,并指明等号成立的条件.
证明:如图3,建立直角坐标系,设∠AO1x=α(0≤α<2π),
∠B1O2x=β(0<β<π),则∠xO2B2=-β,又|O1O2|=1,则点A、B1、B2
三点坐标分别为A( , )、B1( , )、B2( , ),
|
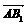 =(
, ),
=(
, ),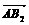 =(
, ).∴|
=(
, ).∴|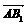 |2= ,|
|2= ,|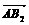 |2= .
|2= .
从而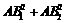 =
,∴
=
,∴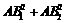 ≥2,且当 时取等号.
≥2,且当 时取等号.
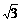 ,-1),则|2a-b|的最大值是 .
,-1),则|2a-b|的最大值是 . ),直线l过点A(3,-1)且与向量a+2b垂直,则直线l的方程为 .
),直线l过点A(3,-1)且与向量a+2b垂直,则直线l的方程为 .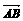 =a,
=a,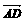 =b,则
=b,则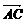 等于
( )
等于
( )
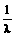 a+b D.a+
a+b D.a+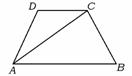 已知a=(-1,3),b=(x,-1),且a∥b,则x等于
( )
已知a=(-1,3),b=(x,-1),且a∥b,则x等于
( )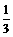 C.-3
D.-
C.-3
D.-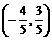 ,点O(0,0)和A(1,-2)在l上的射影分别是
,点O(0,0)和A(1,-2)在l上的射影分别是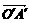 =λe,其中λ为
( )
=λe,其中λ为
( )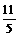 B.
B.