摘要:14.试判断点A,B,C(2,1)是否共线.
网址:http://m.1010jiajiao.com/timu3_id_527210[举报]
网址:http://m.1010jiajiao.com/timu3_id_527210[举报]
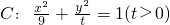 的左顶点,直线l:x=my+1(m∈R)与椭圆C相交于E,F两点,与x轴相交于点B.且当m=0时,△AEF的面积为
的左顶点,直线l:x=my+1(m∈R)与椭圆C相交于E,F两点,与x轴相交于点B.且当m=0时,△AEF的面积为 .
. +
+ =1(a>b>0),称圆心在坐标原点O,半径为
=1(a>b>0),称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2(
的圆是椭圆C的“伴随圆”. 若椭圆C的一个焦点为F2( ,0),其短轴上的一个端点到F2距离为
,0),其短轴上的一个端点到F2距离为 .
. ,求m的值;
,求m的值;