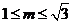0 51620 51628 51634 51638 51644 51646 51650 51656 51658 51664 51670 51674 51676 51680 51686 51688 51694 51698 51700 51704 51706 51710 51712 51714 51715 51716 51718 51719 51720 51722 51724 51728 51730 51734 51736 51740 51746 51748 51754 51758 51760 51764 51770 51776 51778 51784 51788 51790 51796 51800 51806 51814 447348
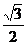 ”
” 是“A>15
是“A>15 ”的( )
”的( )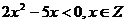 },若P∩Q≠
},若P∩Q≠ ,则m等于( )
,则m等于( )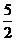 D. 1或2
D. 1或2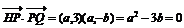 ∴
∴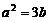 …………1分 设M(x,y)∵
…………1分 设M(x,y)∵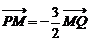 ∴
∴
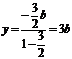 …4分 ∴点M的轨迹曲线C的方程是
…4分 ∴点M的轨迹曲线C的方程是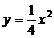 (x≠0) .6分
(x≠0) .6分 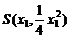 ,
,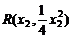 (x1≠x2)
(x1≠x2) ,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分
,即4y = (x1+x2)x-x1x2 ∵A点在SR上,∴4b=(x1+x2)a-x1x2 ①
…………8分 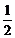 x∴抛物线上S、R处的切线方程为:
x∴抛物线上S、R处的切线方程为: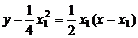 即4
即4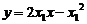 ②
②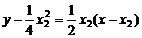 即4
即4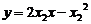 ③
…………11分
③
…………11分 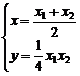 ,代入①得:ax-2y-2b=0
,代入①得:ax-2y-2b=0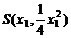 ,
,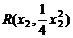 (x1≠x2)
(x1≠x2)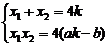 …………9分
…………9分 ,
,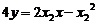 …11分
…11分 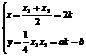 (k为参数)消去k,得:ax-2y-2b=0
(k为参数)消去k,得:ax-2y-2b=0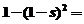
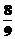 , ∴s=
, ∴s=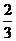 .
………3分
.
………3分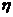 的取值可以是0,1,2.…………………………5分
的取值可以是0,1,2.…………………………5分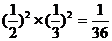 ,
, ,
,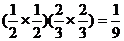 ,
,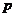 (
(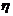 =0)=
=0)=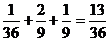 .
…………8分
.
…………8分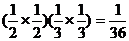 ,
,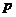 (
(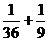 =
=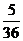 , ……11分
, ……11分 (
(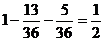 . ……14分
. ……14分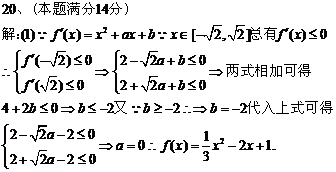
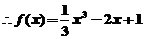

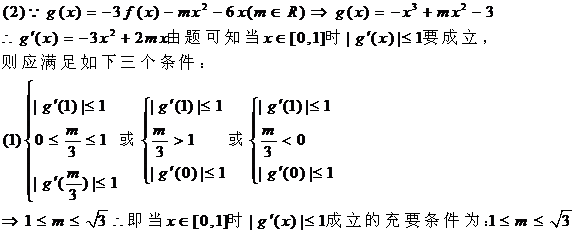
 平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD.
平面ABCD, ∴AC⊥PD, ∴AC⊥平面PBD. ABC中,PA=
ABC中,PA= ,AB=2.
,AB=2.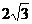 ,∴
,∴ .
.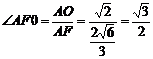 ,∴
,∴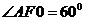 .
. . …………7分
. …………7分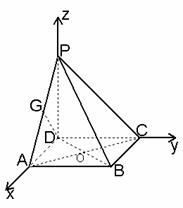 ∵ABCD是正方形,∴AC⊥DB.
∵ABCD是正方形,∴AC⊥DB.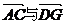 分别是平面PBD与平面PAB的法向量.
分别是平面PBD与平面PAB的法向量.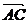 =(-2,2,0).
=(-2,2,0).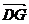 =(1,0,1). …………4分
=(1,0,1). …………4分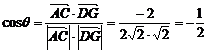 ,
,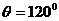 ,∴二面角A-PB-D的大小为
,∴二面角A-PB-D的大小为 (2)解法一: 当点E是线段PB中点时,
(2)解法一: 当点E是线段PB中点时, ∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分
∴PC⊥平面ADHE,即PC⊥平面ADE.
…………14分 .
. (-2,0,2),
(-2,0,2), (2,2,-2),
(2,2,-2), (0,2,-2).
(0,2,-2). .
. 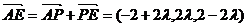 .
.
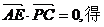 2
2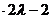 (
(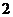 -
-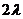 )=0,得
)=0,得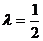 .
.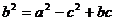 ,得
,得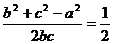
 ,∴
,∴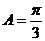 . …………6分
. …………6分
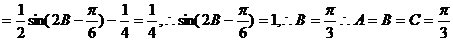
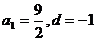 …………4分
…………4分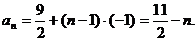 ………………6分
………………6分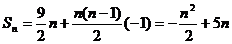 ………………9分
………………9分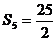 ………………12分
………………12分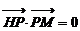 ,
,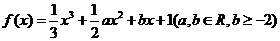 ,
,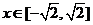 ,总有
,总有 .
.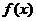 的解析式;
的解析式;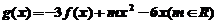 ,求证:当
,求证:当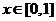 时,
时,  成立的充要条件是:
成立的充要条件是: