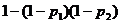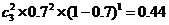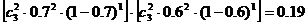0 51646 51654 51660 51664 51670 51672 51676 51682 51684 51690 51696 51700 51702 51706 51712 51714 51720 51724 51726 51730 51732 51736 51738 51740 51741 51742 51744 51745 51746 51748 51750 51754 51756 51760 51762 51766 51772 51774 51780 51784 51786 51790 51796 51802 51804 51810 51814 51816 51822 51826 51832 51840 447348
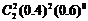
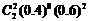 =
=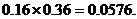
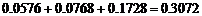
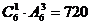 个。四位偶数有:个位是0时有
个。四位偶数有:个位是0时有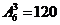 ,个位不是0时有
,个位不是0时有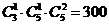 ,共有120+300=420个.
,共有120+300=420个.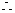 组成的四位数为偶数的概率为
组成的四位数为偶数的概率为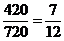
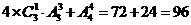 .
.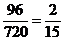
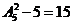 ;千位是4,百位是6时,有
;千位是4,百位是6时,有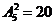 ;千位大于4时,有
;千位大于4时,有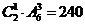 ;故共有240+20+18=278.
;故共有240+20+18=278.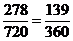
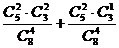 =
=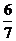 ; (Ⅱ) P=
; (Ⅱ) P=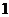 -
-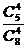 =
=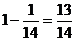
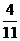
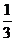 (B)
(B)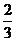 (C)
(C)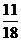 (D)
(D)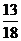
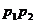 (B)
(B)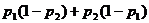 (C)
(C)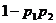 (D)
(D)