摘要:能够将数列转化为等差数列和等比数列再求其通项. [例题讲解] 例题1 (1) 在等差数列{a}中a则n 等于 A 78 B 74 C 70 D 66 (2) 已知方程的四个根组成一个首项为的等比数列,则 = A B 1 C D =.满足xn=f(xn-1), 且x1=f(2).则x10的值为 A B C D (4)设等比数列的公比为q.前n项和为Sn.若Sn+1,Sn.Sn+2成等差数列.则q的值为 . (5) 设函数的反函数为,数列满足则数列的通项为 . (6) 给定.若乘积为整数m.则称k为“希望数 .则区间[1.2005]内所有希望数之和为 . 例题2 在等差数列中.公差的等比中项.已知数列成等比数列.求数列的通项 例题3 已知数列中, 且当时,求数列通项公式. 例题4 数列 中, 是它的前n项的和,并且, ( ) (1) 设 则数列为等比数列; (2) 设,则数列为等差数列; (3)求数列的通项公式以及前n项的和. 例题5 数列中, ,前n项和为Sn.在平面直角坐标系中,点总在曲线上,其中.问: (1) 是否为等比数列?证明你的结论; (2) 若,数列中,,,求; (3) 求.
网址:http://m.1010jiajiao.com/timu3_id_511301[举报]
下面给出的四个命题中:
①对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上是数列an为等差数列的充分不必要条件;
②“m=-2”是直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)与坐标轴有4个交点A(x1,0),B(x2,0),C(0,y1),D(0,y2),则有x1x2-y1y2=0;
④将函数y=cos2x的图象向右平移
个单位,得到函数y=sin(2x-
)的图象.
其中是真命题的有 (将你认为正确的序号都填上).
查看习题详情和答案>>
①对任意的n∈N*,点Pn(n,an)都在直线y=2x+1上是数列an为等差数列的充分不必要条件;
②“m=-2”是直线(m+2)x+my+1=0与“直线(m-2)x+(m+2)y-3=0相互垂直”的必要不充分条件;
③设圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)与坐标轴有4个交点A(x1,0),B(x2,0),C(0,y1),D(0,y2),则有x1x2-y1y2=0;
④将函数y=cos2x的图象向右平移
| π |
| 3 |
| π |
| 6 |
其中是真命题的有
关于数列有下列四个判断:
①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列;
③若数列{an}既是等差数列也是等比数列,则{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则{an}为等差或等比数列;
⑤数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n).
其中正确命题的序号是
查看习题详情和答案>>
①若a,b,c,d成等比数列,则a+b,b+c,c+d也成等比数列;
②若数列{an}是等比数列,则Sn,S2n-Sn,S3n-S2n…也成等比数列;
③若数列{an}既是等差数列也是等比数列,则{an}为常数列;
④数列{an}的前n项的和为Sn,且Sn=an-1(a∈R),则{an}为等差或等比数列;
⑤数列{an}为等差数列,且公差不为零,则数列{an}中不会有am=an(m≠n).
其中正确命题的序号是
②③④⑤
②③④⑤
.(请将正确命题的序号都填上)已知数列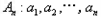 ,如果数列
,如果数列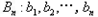 满足
满足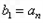 ,
,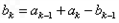 ,其中
,其中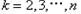 ,则称
,则称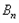 为
为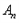 的“生成数列”.
的“生成数列”.
(1)若数列 的“生成数列”是
的“生成数列”是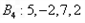 ,求
,求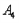 ;
;
(2)若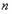 为偶数,且
为偶数,且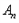 的“生成数列”是
的“生成数列”是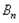 ,证明:
,证明: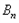 的“生成数列”是
的“生成数列”是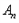 ;
;
(3)若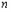 为奇数,且
为奇数,且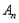 的“生成数列”是
的“生成数列”是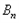 ,
,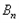 的“生成数列”是
的“生成数列”是 ,….依次将数列
,….依次将数列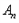 ,
,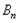 ,
,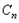 ,…的第
,…的第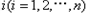 项取出,构成数列
项取出,构成数列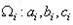 ,…,探究:数列
,…,探究:数列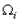 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.
查看习题详情和答案>>
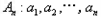 ,如果数列
,如果数列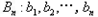 满足
满足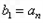 ,
,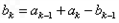 ,其中
,其中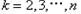 ,则称
,则称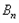 为
为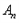 的“生成数列”.
的“生成数列”.(1)若数列
 的“生成数列”是
的“生成数列”是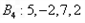 ,求
,求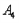 ;
;(2)若
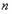 为偶数,且
为偶数,且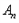 的“生成数列”是
的“生成数列”是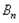 ,证明:
,证明: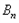 的“生成数列”是
的“生成数列”是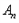 ;
;(3)若
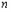 为奇数,且
为奇数,且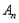 的“生成数列”是
的“生成数列”是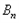 ,
,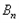 的“生成数列”是
的“生成数列”是 ,….依次将数列
,….依次将数列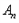 ,
,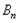 ,
,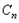 ,…的第
,…的第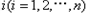 项取出,构成数列
项取出,构成数列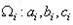 ,…,探究:数列
,…,探究:数列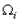 是否为等差数列,并说明理由.
是否为等差数列,并说明理由.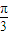 个单位,得到函数
个单位,得到函数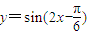 的图象.
的图象.