19. (本小题满分14分)
(1)
|
长度ξμm |
29 |
30 |
31 |
|
P |
0.3 |
0.5 |
0.2 |
|
宽度ημm |
19 |
20 |
21 |
|
P |
0.3 |
0.4 |
0.3 |
4分
(2)P(ζ = 96) = 0.3´0.3 = 0.09;
P(ζ = 98) = 0.3´0.4 + 0.5´0.3 = 0.27;
P(ζ = 100) = 0.5´0.4 + 0.2´0.3 + 0.3´0.3 = 0.35;
P(ζ = 102) = 0.2´0.4 + 0.5´0.3 = 0.23;
P(ζ = 104) = 0.2´0.3 = 0.06.
得,周长分布律如下表所示
|
周长μ μm |
96 |
98 |
100 |
102 |
104 |
|
P |
0.09 |
0.27 |
0.35 |
0.23 |
0.06 |
6分
(3)方法1(利用周长的分布计算)
Eμ= 96×0.09+98×0.27+100×0.35+102×0.23+104×0.06=99.8 4分
方法2(利用矩形长与宽的期望计算)
由长和宽的分布率可以算得
Eξ=29×P(ξ=29)+30×P(ξ=30)+31×P(ξ=31)
=29×0.3+30×0.5+31×0.2=29.9
Eη=19×P(η=19)+20×P(η=20)+21×P(η=21)
=19×0.3+20×0.4+21×0.3=20
由期望的性质可得
Eμ=2(Eξ+Eη)=2×(29.9+20)=99.8 4分
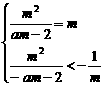 , 得
, 得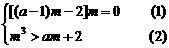 2分
2分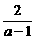 ,
,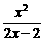 ( x ¹ 1).
3分
( x ¹ 1).
3分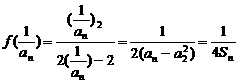
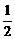 ak(1 – ak) + a k + 1 =
ak(1 – ak) + a k + 1 = 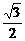 b |2 = |
(
b |2 = |
(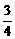 3 分
3 分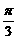 ) +
) +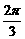 , ∴–
, ∴–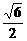 ).
2分
).
2分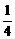 | a |2 –
| a |2 – 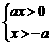 ,得a > 0 , x > 0 . 3
分
,得a > 0 , x > 0 . 3
分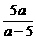 . 2分
. 2分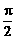 < C – A <
< C – A < 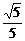 . 14. 0 < a £
. 14. 0 < a £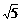 – 2 (或q < x £ p , 其中q > 0, p£
– 2 (或q < x £ p , 其中q > 0, p£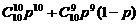 .
.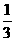 .
.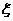 的期望与方差.
的期望与方差.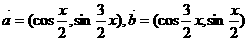 且
且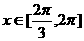 .
.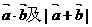 ;
;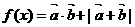 的最值.
的最值.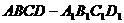 中,
中,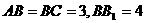 连接
连接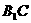 过B作
过B作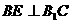 交
交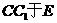 ,交
,交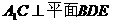 ;
; 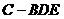 的体积;
的体积;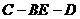 的正切值.
的正切值. 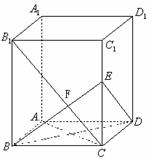
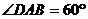 的菱形,
的菱形,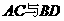 相交于
相交于 点,
点, 与
与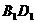 相交于
相交于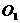 点,点
点,点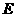 是
是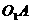 的中点.
的中点.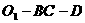 的大小;
的大小;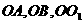 为
为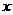 轴,
轴,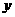 轴,
轴,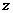 轴的正半轴建立空间直角坐标系,求点
轴的正半轴建立空间直角坐标系,求点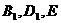 的坐标,并求异面直线
的坐标,并求异面直线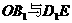 所成角的大小.
所成角的大小.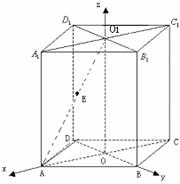
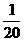 x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?
x,该洗车行每年的其他费用是1万元.问:洗车行A从今年开始至少经过多少年才能收回购买净化器的成本?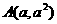 为抛物线
为抛物线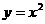 上任意一点,直线
上任意一点,直线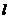 为过点
为过点 的切线,设直线
的切线,设直线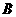 .
.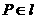 ,且
,且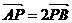 .
.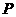 的轨迹方程;
的轨迹方程;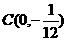 到动直线
到动直线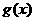 与函数
与函数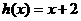 图像关于
图像关于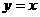 对称.且函数
对称.且函数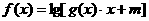 ,(其中
,(其中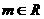 ,
, 为常数)
为常数)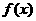 的定义域;
的定义域;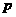 ,使得
,使得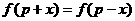 ,若存在,请求出
,若存在,请求出 ?并证明你的结论.
?并证明你的结论.