(15) 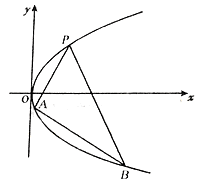 如图,过抛物线y2=2px (p>0) 上一定点P(x0, y0)
(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).
如图,过抛物线y2=2px (p>0) 上一定点P(x0, y0)
(y0>0),作两条直线分别交抛物线于A(x1,y1),B(x2,y2).
(I)求该抛物线上纵坐标为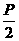 的点到其焦点F的距离;
的点到其焦点F的距离;
(II)当PA与PB的斜率存在且倾斜角互补时,
求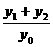 的值,并证明直线AB的斜率是非零常数。
的值,并证明直线AB的斜率是非零常数。
(16) 设椭圆方程为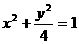 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足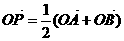 ,点N的坐标为
,点N的坐标为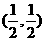 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(Ⅰ)动点P的轨迹方程;
(Ⅱ)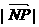 的最小值与最大值.
的最小值与最大值.
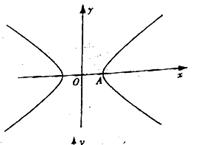 (17) 已知双曲线的中心在原点,右顶点为A(1,0)点P、Q
(17) 已知双曲线的中心在原点,右顶点为A(1,0)点P、Q
在双曲线的右支上,支M(m,0)到直线AP的距离为1.
(Ⅰ)若直线AP的斜率为k,且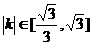 ,求实数m的
,求实数m的
取值范围;
(Ⅱ)当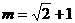 时,ΔAPQ的内心恰好是点M,求此双曲
时,ΔAPQ的内心恰好是点M,求此双曲
线的方程.
(18)椭圆的中心是原点O,它的短轴长为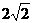 ,相应于焦点F(c,0)(
,相应于焦点F(c,0)(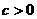 )的准线
)的准线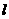 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(Ⅰ)求椭圆的方程及离心率;
(Ⅱ)若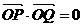 ,求直线PQ的方程;
,求直线PQ的方程;
(Ⅲ)设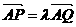 (
(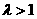 ),过点P且平行于准线
),过点P且平行于准线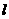 的直线与椭圆相交于另一点M,
的直线与椭圆相交于另一点M,
证明: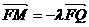 .
.
第十三单元
一选择题: 1.D 2.C 3.A 4.B 5.B 6.C 7.D 8.C 9.B 10.D
二填空题: 11.
3, 12. [-1,3],
13. 4, 14. 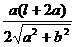 .
.
 三解答题
三解答题
(15)解(I)当y=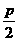 时,x=
时,x=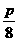 ,又抛物线y2=2px
,又抛物线y2=2px
的准线方程为x=-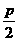 ,由抛物线定义得,所以
,由抛物线定义得,所以
距离为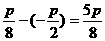 .
.
(II)设直线PA的斜率为kPA,直线PB的斜率为kPB.
由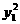 =2px1,
=2px1,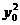 =2px0相减得
=2px0相减得
(y1-y0)(y1+y0)=2p(x1-x0)
故 kPA=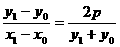 (x1≠x0)同理可得 kPB=
(x1≠x0)同理可得 kPB=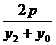 (x2≠x0)由PA,PB
(x2≠x0)由PA,PB
倾斜角互补知kPA=-kPB,即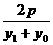 =-
=-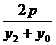 ,所以y1+y2=-2y0,故
,所以y1+y2=-2y0,故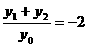
设直线AB的斜率为kAB. 由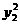 =2px2,
=2px2,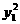 =2px1相减得(y2-y1)(y2+y1)=2p(x2-x1),
=2px1相减得(y2-y1)(y2+y1)=2p(x2-x1),
所以kAB=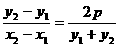 (x1≠x2)将 y1+y2=-2y0 (y0>0
)代入得kAB=
(x1≠x2)将 y1+y2=-2y0 (y0>0
)代入得kAB=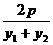
=-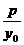 ,所以kAB是非零常数.
,所以kAB是非零常数.
(16) (Ⅰ)解法一:直线l过点M(0,1)设其斜率为k,则l的方程为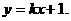
|
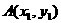 、
、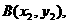 由题设可得点A、B的坐标
由题设可得点A、B的坐标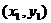 、
、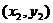 是方程组
是方程组
|
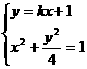 的解.将①代入②并化简得,
的解.将①代入②并化简得,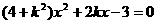 ,所以
,所以
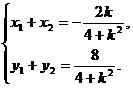 于是
于是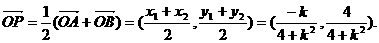
设点P的坐标为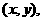 则
则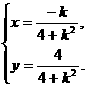 消去参数k得
消去参数k得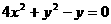 ③ 当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方程为
③ 当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方程为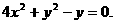
解法二:设点P的坐标为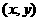 ,因
,因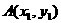 、
、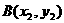 在椭圆上,所以
在椭圆上,所以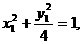 ④
④ 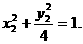 ⑤. ④-⑤得
⑤. ④-⑤得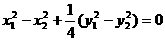 ,所以
,所以
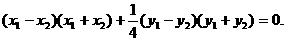 当
当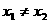 时,有
时,有
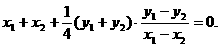 ⑥并且
⑥并且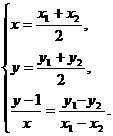 ⑦ 将⑦代入⑥并整理得
⑦ 将⑦代入⑥并整理得
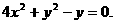 ⑧. 当
⑧. 当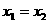 时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)也满足⑧,所以点P的轨迹方程为
时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)也满足⑧,所以点P的轨迹方程为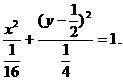
(Ⅱ)解:由点P的轨迹方程知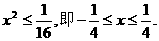 所以
所以
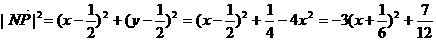
故当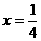 ,
,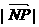 取得最小值,最小值为
取得最小值,最小值为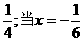 时,
时,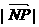 取得最大值,最大值为
取得最大值,最大值为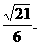
(17) 解: (Ⅰ)由条件得直线AP的方程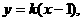 即
即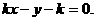 因为点M到直线AP的距离为1,∵
因为点M到直线AP的距离为1,∵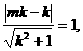 即
即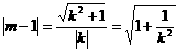 .∵
.∵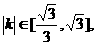
∴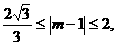 解得
解得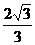 +1≤m≤3或--1≤m≤1--
+1≤m≤3或--1≤m≤1--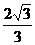 . ∴m的取值范围是
. ∴m的取值范围是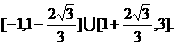 (Ⅱ)可设双曲线方程为
(Ⅱ)可设双曲线方程为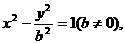 由
由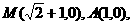 得
得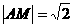 .又因为M是ΔAPQ的内心,M到AP的距离为1,所以∠MAP=45º,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1。因此,
.又因为M是ΔAPQ的内心,M到AP的距离为1,所以∠MAP=45º,直线AM是∠PAQ的角平分线,且M到AQ、PQ的距离均为1。因此,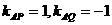 (不妨设P在第一象限)直线PQ方程为
(不妨设P在第一象限)直线PQ方程为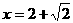 。直线AP的方程y=x-1,∴解得P的坐标是(2+
。直线AP的方程y=x-1,∴解得P的坐标是(2+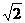 ,1+
,1+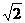 ),将P点坐标代入
),将P点坐标代入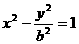 得,
得,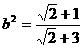 所以所求双曲线方程为
所以所求双曲线方程为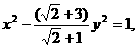 即
即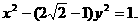
(18)(Ⅰ)解:由题意,可设椭圆的方程为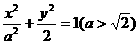 .由已知得
.由已知得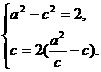 解得
解得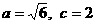 所以椭圆的方程为
所以椭圆的方程为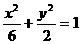 ,离心率
,离心率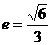 .(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为
.(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为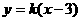 .由方程组
.由方程组
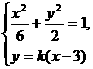 得
得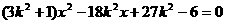 依题意
依题意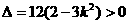 ,得
,得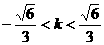 .设
.设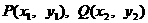 ,则
,则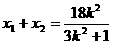 , ①
, ①
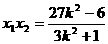 . ② 由直线PQ的方程得
. ② 由直线PQ的方程得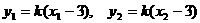 .于是
.于是
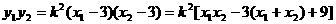 . ③ ∵
. ③ ∵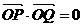 ,∴
,∴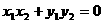 . ④. 由①②③④得
. ④. 由①②③④得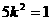 ,从而
,从而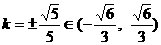 .
.
所以直线PQ的方程为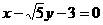 或
或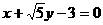 . (Ⅲ)证明:
. (Ⅲ)证明: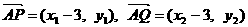 .由已知得方程组
.由已知得方程组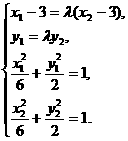
注意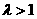 ,解得
,解得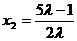 . 因
. 因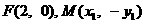 ,
,
故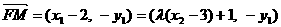
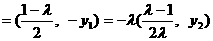 .
.
而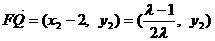 ,所以
,所以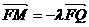 .
.
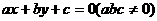 与圆
与圆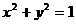 相切,则三条边长分别为
相切,则三条边长分别为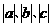 的三角形( )
的三角形( )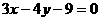 与圆
与圆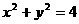 的位置关系是( )
的位置关系是( )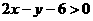 表示的平面区域在直线
表示的平面区域在直线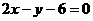 的( )
的( )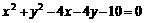 上的点到直线
上的点到直线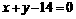 的最大距离与最小距离的差是( )
的最大距离与最小距离的差是( )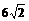 D.
D. 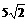
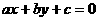 同时要经过第一、第二、第四象限,则
同时要经过第一、第二、第四象限,则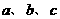 应满足( )
应满足( )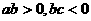 B.
B.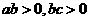 C.
C.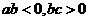 D.
D.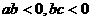
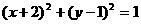 关于原点对称,则圆C的方程是( )
关于原点对称,则圆C的方程是( )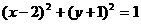 B.
B.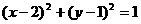
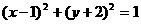 D.
D.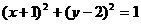
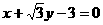 的倾斜角是( )
的倾斜角是( )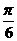 B.
B.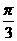 C.
C.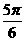 D.
D.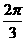
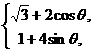 (0≤θ≤2π)恒有公共点,则b的取值范围是
.
(0≤θ≤2π)恒有公共点,则b的取值范围是
.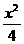 +y2=1的两个焦点, P是该椭圆上的一个动点, 则|PF1|·|PF2|的最大值是
.
+y2=1的两个焦点, P是该椭圆上的一个动点, 则|PF1|·|PF2|的最大值是
.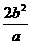 )的线段AB的端点在双曲线b2x2-a2y2=a2b2的右支上, 则AB中点M的横坐标的最小值为
.
)的线段AB的端点在双曲线b2x2-a2y2=a2b2的右支上, 则AB中点M的横坐标的最小值为
.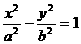 (0<a<b)的半焦距c, 直线l过(a, 0), (0, b)两点. 已知原点到直线l的距离为
(0<a<b)的半焦距c, 直线l过(a, 0), (0, b)两点. 已知原点到直线l的距离为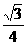 c, 则双曲线的离心率为
(
)
c, 则双曲线的离心率为
(
)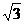 C
C 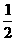 , 那么m的值等于
(
)
, 那么m的值等于
(
)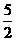 B
B 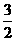 C 2
D 3
C 2
D 3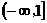 D (-∞, 0)
D (-∞, 0)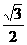 B
B 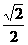 C
C 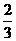 D
D