摘要:. 证明 只需对任意.证明不等式成立即可. 记.则 . .. . 把上面这n个等式相加.并利用可得 . 由Cauchy 不等式可得 . 所以 .
网址:http://m.1010jiajiao.com/timu3_id_502854[举报]
已知函数f(x)=2x,g(x)=-x2+2x+b(b∈R),记h(x)=f(x)-
.
(Ⅰ)判断h(x)的奇偶性,并证明;
(Ⅱ)对任意x∈[1,2],都存在x1,x2∈[1,2],使得f(x)≤f(x1),g(x)≤g(x2).若f(x1)=g(x2),求实数b的值;
(Ⅲ)若2xh(2x)+mh(x)≥0对于一切x∈[1,2]恒成立,求实数m的取值范围.
查看习题详情和答案>>
| 1 | f(x) |
(Ⅰ)判断h(x)的奇偶性,并证明;
(Ⅱ)对任意x∈[1,2],都存在x1,x2∈[1,2],使得f(x)≤f(x1),g(x)≤g(x2).若f(x1)=g(x2),求实数b的值;
(Ⅲ)若2xh(2x)+mh(x)≥0对于一切x∈[1,2]恒成立,求实数m的取值范围.
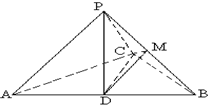 如图,已知三棱锥P-ABC中,PA⊥PC,D为AB中点,M为PB的中点,且AB=2PD.
如图,已知三棱锥P-ABC中,PA⊥PC,D为AB中点,M为PB的中点,且AB=2PD.(I)求证:DM∥面PAC;
(II)找出三棱锥P-ABC中一组面与面垂直的位置关系,并给出证明(只需找到一组即可)
我们给出如下定义:对函数y=f(x),x∈D,若存在常数C(C∈R),对任意的x1∈D,存在唯一的x2∈D,使得
=C,则称函数f(x)为“和谐函数”,称常数C为函数f(x)的“和谐数”.
(1)判断函数f(x)=x+1,x∈[-1,3]是否为“和谐函数”?答:
(2)请先学习下面的证明方法:
证明:函数g(x)=lgx,x∈[10,100]为“和谐函数”,
是其“和谐数”.
证明过程如下:对任意x1∈[10,100],令
=
,即
=
,
得x2=
.∵x1∈[10,100],∴x2=
∈[10,100].即对任意x1∈[10,100],存在唯一的x2=
∈[10,100],使得
=
.∴g(x)=lgx为“和谐函数”,
是其“和谐数”.
参照上述证明过程证明:函数h(x)=2x,x∈(1,3)为“和谐函数”;
(3)写出一个不是“和谐函数”的函数,并作出证明.
查看习题详情和答案>>
| f(x1)+f(x2) |
| 2 |
(1)判断函数f(x)=x+1,x∈[-1,3]是否为“和谐函数”?答:
是
是
.(填“是”或“否”)如果是,写出它的一个“和谐数”:2
2
.(2)请先学习下面的证明方法:
证明:函数g(x)=lgx,x∈[10,100]为“和谐函数”,
| 3 |
| 2 |
证明过程如下:对任意x1∈[10,100],令
| g(x1)+g(x2) |
| 2 |
| 3 |
| 2 |
| lgx1+lgx2 |
| 2 |
| 3 |
| 2 |
得x2=
| 1000 |
| x1 |
| 1000 |
| x1 |
| 1000 |
| x1 |
| g(x)+g(x2) |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
参照上述证明过程证明:函数h(x)=2x,x∈(1,3)为“和谐函数”;
(3)写出一个不是“和谐函数”的函数,并作出证明.
 ,只需证明
,只需证明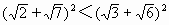 ”所依据的理论是:不等式的性质定理
”所依据的理论是:不等式的性质定理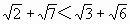 ,只需证明
,只需证明 ”所依据的理论是:不等式的性质定理
”所依据的理论是:不等式的性质定理