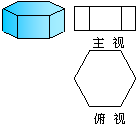
0 49154 49162 49168 49172 49178 49180 49184 49190 49192 49198 49204 49208 49210 49214 49220 49222 49228 49232 49234 49238 49240 49244 49246 49248 49249 49250 49252 49253 49254 49256 49258 49262 49264 49268 49270 49274 49280 49282 49288 49292 49294 49298 49304 49310 49312 49318 49322 49324 49330 49334 49340 49348 447348
 C.三边的垂直平分线的交点 D.三条中线的交点
C.三边的垂直平分线的交点 D.三条中线的交点 A. 5 B.±5 C.
A. 5 B.±5 C.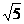 D.±
D.±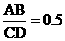 ,即CH+DH=2AB=2CH
,即CH+DH=2AB=2CH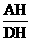 =2,
=2,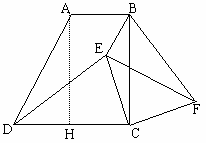 在△EDC和△FBC中,
在△EDC和△FBC中,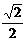 EF. ………………………………………5分
EF. ………………………………………5分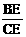 =0.5 ,
=0.5 , 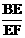 =
=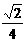 .
…………………………
.
………………………… ……………6分
……………6分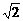 ,EF= 4,则BF=
,EF= 4,则BF=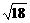 .
.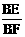 =
=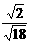 =
=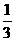 .
………………………………………7分
.
………………………………………7分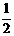 x,
CE=1-
x,
CE=1-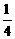 x,
AF=1-(
x,
AF=1-(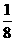 x+
x+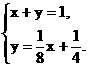 …………………………………………3分
…………………………………………3分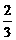 .
……………………………………………4分
.
……………………………………………4分  ∴EF=
∴EF=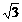 CF=
CF=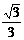 . …………………………………………5分
. …………………………………………5分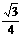 .
……………………………7分
.
……………………………7分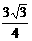 ≤ m <
≤ m <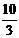 >0,与“k<0”不符.
>0,与“k<0”不符.
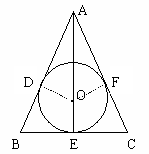 ⑴ 是
…………………………………………1分
⑴ 是
…………………………………………1分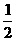 AB=2,
AB=2,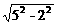 =
=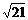 .
………………………………………3分
.
………………………………………3分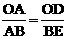 ,
………………………………………………4分
,
………………………………………………4分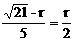 .
.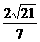 .
. 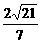 .
……………………………………………5分
.
……………………………………………5分 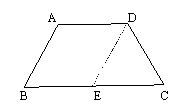 作DE∥AB交BC与E,则∠DEC=∠B=60°, ………………………2分
作DE∥AB交BC与E,则∠DEC=∠B=60°, ………………………2分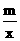 ,
,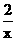 .
………………………………2分
.
………………………………2分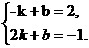 ……………………………………………4分
……………………………………………4分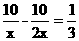 .
……………………………………2分
.
……………………………………2分