0 49027 49035 49041 49045 49051 49053 49057 49063 49065 49071 49077 49081 49083 49087 49093 49095 49101 49105 49107 49111 49113 49117 49119 49121 49122 49123 49125 49126 49127 49129 49131 49135 49137 49141 49143 49147 49153 49155 49161 49165 49167 49171 49177 49183 49185 49191 49195 49197 49203 49207 49213 49221 447348
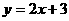 中,
中,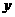 随
随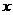 的增大而 (填“增大”或“减小”),当
的增大而 (填“增大”或“减小”),当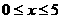 时,y的最小值为 .
时,y的最小值为 .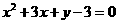 ,
, _______.
_______.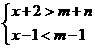 的解集为
的解集为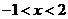 ,则
,则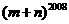 = .
= .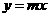 与双曲线
与双曲线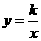 的一个交点A的坐标为
的一个交点A的坐标为 ,则
,则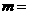 ,
,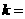 ,它们的另一个交点坐标是
。
,它们的另一个交点坐标是
。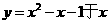 轴的一个点为(m,0)则代数式
轴的一个点为(m,0)则代数式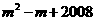 的值为( )
的值为( ) A.―2―
B.―1―
A.―2―
B.―1― C.―2+
D.1+
C.―2+
D.1+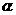 (0°<
(0°<
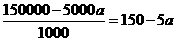 ,可得:
,可得: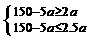 解得
解得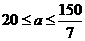 。又a是正整数,所以a=20或21;当a=20时,b=50;当a=21时,b=45。故共有两个方案:方案一,建室内车位20个,露天车位50个;方案二,建室内车位21个,露天车位45个。
。又a是正整数,所以a=20或21;当a=20时,b=50;当a=21时,b=45。故共有两个方案:方案一,建室内车位20个,露天车位50个;方案二,建室内车位21个,露天车位45个。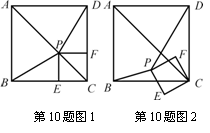 如图(1),已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.
如图(1),已知P为正方形ABCD的对角线AC上一点(不与A、C重合),PE⊥BC于点E,PF⊥CD于点F.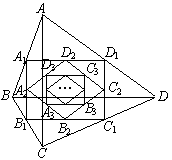 (1)证明:四边形A1B1C1D1是矩形;
(1)证明:四边形A1B1C1D1是矩形;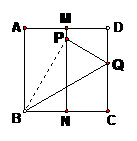 如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PQ.
如图,有一块面积为1的正方形ABCD,M、N分别为AD、BC边的中点,将C点折至MN上,落在点P的位置,折痕为BQ,连结PQ.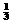 .
. (3)求△AMN的面积的最大值,并判断取最大值时△AMN的形状.
(3)求△AMN的面积的最大值,并判断取最大值时△AMN的形状.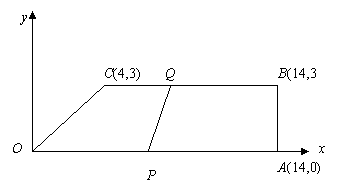 (4)设四边形OPQC的面积为y,求出当 x﹥2.5时y与x的函数关系式;并求出y的最大值;
(4)设四边形OPQC的面积为y,求出当 x﹥2.5时y与x的函数关系式;并求出y的最大值; 如图,梯形ABCD中,AD∥BC,M、N、P、Q分别为AD、BC、BD、AC的中点。求证:MN和PQ互相平分。
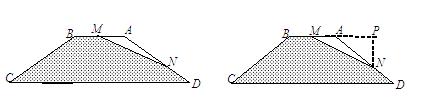
如图,梯形ABCD中,AD∥BC,M、N、P、Q分别为AD、BC、BD、AC的中点。求证:MN和PQ互相平分。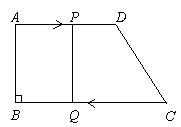 如图,梯形ABCD中,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1m/s的速度移动,点Q从C点开始沿CB边向B以2m/s的速度移动,如果P、Q分别从A、C同时出发,设移动时间为t秒,求:
如图,梯形ABCD中,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1m/s的速度移动,点Q从C点开始沿CB边向B以2m/s的速度移动,如果P、Q分别从A、C同时出发,设移动时间为t秒,求: