21.(本题满分10分)
(1)
|
|
第1次 |
第2次 |
第3次 |
第4次 |
………… |
第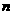 次 次 |
 |
 |
 |
 |
 |
………… |
|
|
1 |
5 |
17 |
53 |
161 |
………… |
|
(前四空每空各0.5 分,第五空1分)
(2)
后一个三角形的个数为前一个三角形个数的3倍加2
(答案允许不同,言之成立即可,满分2分)
(3)根据你的判断,经过第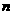 次变换后,三角形的个数是
次变换后,三角形的个数是 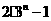 .
.
(第三小题满分3分)
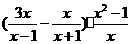 其中
其中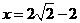
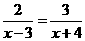
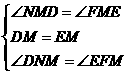
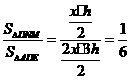
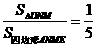 - 4分-
- 4分-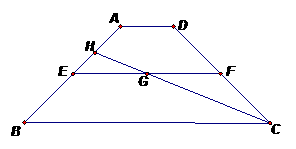 则:
则: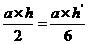
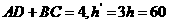 - 5分-
- 5分-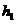
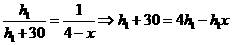
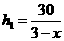 - 6分-
- 6分-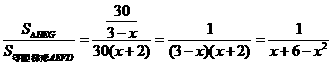 - 7分-
- 7分-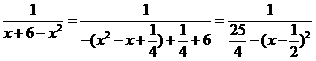 - 8分-
- 8分-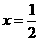 时,
时,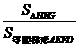 的比值最大,为
的比值最大,为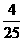
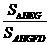 的比值最大,为
的比值最大,为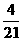 - 9分-
- 9分-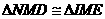 得:
得: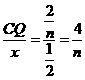
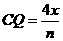 - 10分-
- 10分-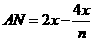
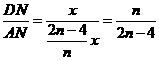
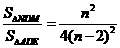
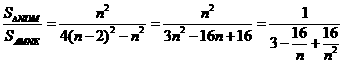 - 11分-
- 11分-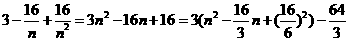
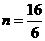 时, 为函数
时, 为函数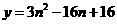 的对称轴,
的对称轴,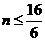 时,函数单调递减,故此时
时,函数单调递减,故此时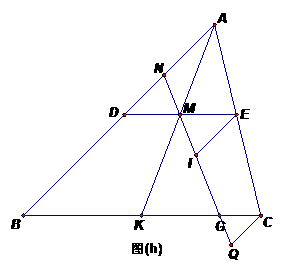
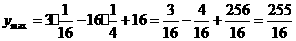 - 12分-
- 12分-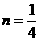 ,
,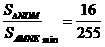 - 13分-
- 13分-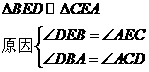 -1分-
-1分-
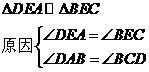 -2分-
-2分-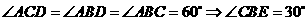
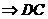 ∥
∥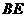
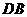 ∥
∥
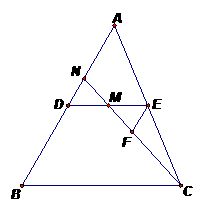 ∴ BC2的最小值是5.
- 12分-
∴ BC2的最小值是5.
- 12分-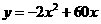 ;15;450.
-6分-
;15;450.
-6分-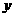 取最大值时的设计示意图分别为:
取最大值时的设计示意图分别为: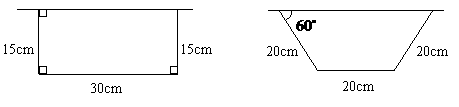
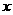 大于30cm时,符合题意的等腰梯形不存在,所以
大于30cm时,符合题意的等腰梯形不存在,所以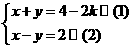 ,(1)+(2)得:
,(1)+(2)得: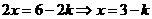 -2分-
-2分-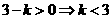 -3分-
-3分-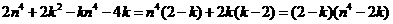 -4分-
-4分-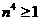
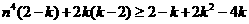 -5分-
-5分-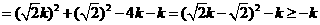
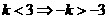 -6分-
-6分-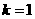 时,
时,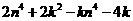
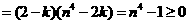
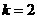 时,
时,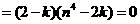 -7分-
-7分-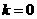 时,
时,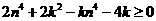 -8分-
-8分-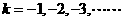 时,
时,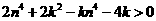 -9分-
-9分-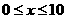 时,
时,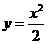 -1分-
-1分-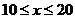 时,
时,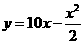 -2分-
-2分-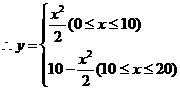 -3分-
-3分-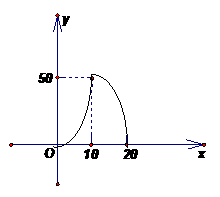
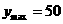 -7分-
-7分-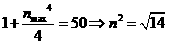 -9分-
-9分-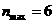 -10分-
-10分-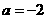 ,则
,则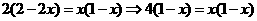 -1分-
-1分-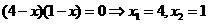 -2分-
-2分-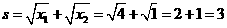 -3分-
-3分-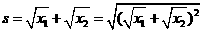 -4分-
-4分-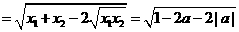 -5分-
-5分-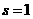
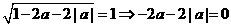
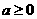 -6分-
-6分-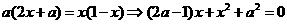
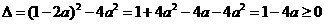
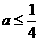 -7分-
-7分-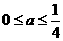 -8分-
-8分-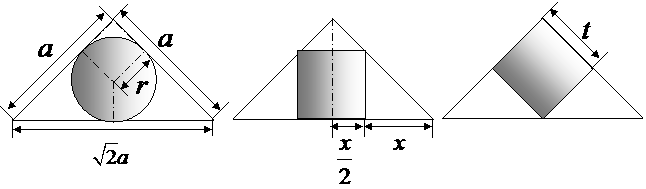 (本题满分7分)
(本题满分7分) 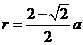 -1分-
-1分-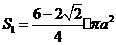 -2分-
-2分-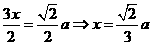 -3分-
-3分-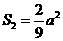 -4分-
-4分-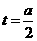 -5分-
-5分-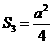 -6分-
-6分-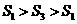 ,故选择方案一.
-7分-
,故选择方案一.
-7分-