90、(2009年淄博市)某中学共有学生2000名,各年级男女生人数如下表:
|
|
六年级 |
七年级 |
八年级 |
九年级 |
|
男生 |
250 |
z |
254 |
258 |
|
女生 |
x |
244 |
y |
252 |
若从全校学生中任意抽一名,抽到六年级女生的概率是0.12;若将各年级的男、女生人数制作成扇形统计图,八年级女生对应扇形的圆心角为44.28°.
(1)求x,y,z的值;
(2)求各年级男生的中位数;
(3)求各年级女生的平均数;
(4)从八年级随机抽取36名学生参加社会实践活动,求抽到八年级某同学的概率.
解: (1)由题意:
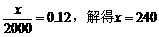 (人).
(人).
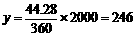 (人).
(人).
z=2000-250-240-244-254-246-258-252=256(人).
(2)各年级男生的中位数为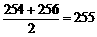 (人).
(人).
(3)各年级女生的平均数为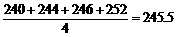 (人).
(人).
(4)抽到八年级某同学的概率为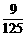 .
.
86、(2009年内蒙古包头)某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
|
测试项目 |
测试成绩 |
||
|
甲 |
乙 |
丙 |
|
|
教学能力 |
85 |
73 |
73 |
|
科研能力 |
70 |
71 |
65 |
|
组织能力 |
64 |
72 |
84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
[答案]本题考查平均数和加权平均数的知识及它们在生活中的应用,特别是加权平均数尤为重要。
(1)甲的平均成绩为: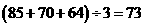
乙的平均成绩为: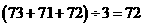
丙的平均成绩为: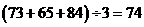
∴候选人丙将被录用。
(2)甲的测度成绩为: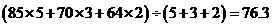
乙的测度成绩为: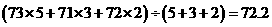
丙的测度成绩为: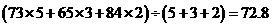
∴候选人甲将被录用。
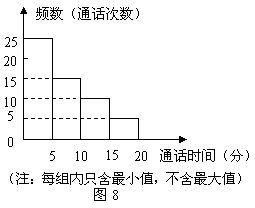
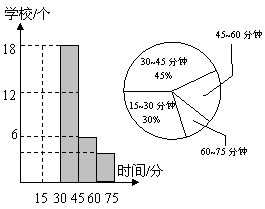
82、(2009年上海市)为了了解某校初中男生的身体素质状况,在该校六年级至九年级共四个年级的男生中,分别抽取部分学生进行“引体向上”测试.所有被测试者的“引体向上”次数情况如表一所示;各年级的被测试人数占所有被测试人数的百分率如图5所示(其中六年级相关数据未标出).
|
次数 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
人数 |
1 |
1 |
2 |
2 |
3 |
4 |
2 |
2 |
2 |
0 |
1 |
表一
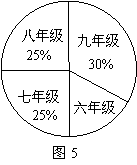

根据上述信息,回答下列问题(直接写出结果):
(1)六年级的被测试人数占所有被测试人数的百分率是 ;
(2)在所有被测试者中,九年级的人数是 ;
(3)在所有被测试者中,“引体向上”次数不小于6的人数所占的百分率是 ;
(4)在所有被测试者的“引体向上”次数中,众数是 .
[关键词]统计图表 众数 频率
[答案](1)20%
(2)6人
(3)35%
(4)5次
81、(2009年黄冈市)为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据如下表(单位:秒):
|
编号 类型 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
|
甲种电子钟 |
1 |
-3 |
-4 |
4 |
2 |
-2 |
2 |
-1 |
-1 |
2 |
|
乙种电子钟 |
4 |
-3 |
-1 |
2 |
-2 |
1 |
-2 |
2 |
-2 |
1 |
(1)计算甲、乙两种电子钟走时误差的平均数;
(2)计算甲、乙两种电子钟走时误差的方差;
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你买哪种电子钟?为什么?
[关键词]平均数 方差 稳定性
[答案](1)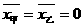
(2)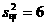
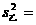 4.8
4.8
买乙种电子钟,因为乙种电子钟更稳定.

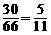 .
.

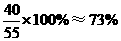
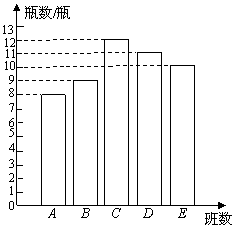

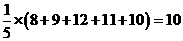 (瓶).
(瓶).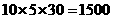 (瓶).
(瓶). (元),
(元), (元).
(元).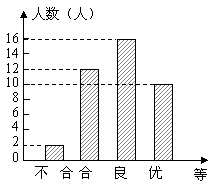

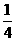 ;
;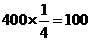 (人).
(人).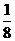 ,求每张乒乓球门票的价格。
,求每张乒乓球门票的价格。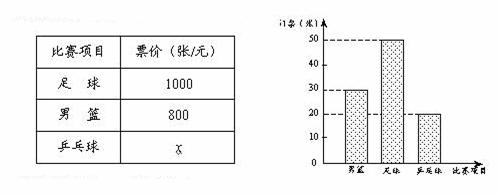
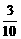
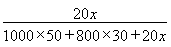
 = .
= . 

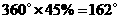 ;
; ;图略.
;图略.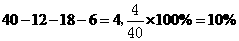 .
.