3.图表分析法
例1某服装厂现有A种布料70m,B种布料52m,现计划用这两种布料生产M、N两种型号的时装80套。已知做一套M型号的时装需要A种布料0.6m,B种布料0.9m,可获利45元,做一套N型号的时装需要A种布料1.1m,B种布料0.4m,可获利50元。若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装所获的总利润为y元。(1)求y与x的函数关系式,并求出自变量x的取值范围;(2)该服装厂在生产这批时装中,当生产N型号的时装多少套时,所获利润最大?最大利润是多少?
解析:虽然题目看起来与前面的调运问题联系不大,但这道题中同样也出现了较多量及数据,因而同样可利用图表来整理数据,而且也方便易行。对于第一个问题的函数关系,根据题中已设好的未知数及相关条件易得“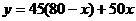 ”,化简即“
”,化简即“ ”。这道题的难点在于确定自变量x的取值范围,对于这个问题,可用两种方法进行分析。
”。这道题的难点在于确定自变量x的取值范围,对于这个问题,可用两种方法进行分析。
分析方法一:列表法
|
每套时装用料 |
(80-x)套 M型时装 |
x套 N型时装 |
总用料量 |
|
A种布料(共70m) |
0.6 |
1.1 |
0.6(80-x)+1.1x |
|
B种布料(共52m) |
0.9 |
0.4 |
0.9(80-x)+0.4x |
上表格形式简单,内容清晰,完成表格并不困难,重要的是让学生理解求x范围的关键在于两种型号的时装每种布料用量和不能超过所提供的布料,由此得出两个不等式“0.6(80-x)+1.1x≤70,0.9(80-x)+0.4x≤52”。解两个不等式即可求出x的取值范围为“40≤x≤44”。其实到这里问题也就基本解决了,因为第二个问题可由刚才的结论直接求得。





和例1相比,这个示意图在结构上更为简洁,每种型号的时装都用到两种布料,图中箭头指向是该布料的使用情况,如:由A种布料引出的两根箭头表示A种布料分别用于M型时装每套0.6m,用于N型时装每套1.1m,而M型时装共生产(80-x)套,这样A种布料一共使用了[0.6(80-x)+1.1x]m,同理可得,B种布料一共用了[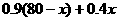 ]m。通过这个示意图也很容易求出x的取值范围。具体解题过程如下:
]m。通过这个示意图也很容易求出x的取值范围。具体解题过程如下:
答案:(1)由题意得 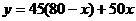
化简可得 
又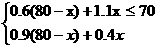
解之得 40≤x≤44
(2)当x=44时,y=5×44+3600=3820
∴当生产N型号的时装44套时,所获利润最大,最大利润是3820元。
方法点拨:通过图表将题目中的各数据间的关系更为简洁的体现出来,使得题意更加明朗,各个量之间的关系也变得国家更加清晰,从而降低了解题的难度。再结合问题,设出未知数后,利用图表所反映出来的关系,可以把各个相关量全部表示出来,最后根据相等关系,不难列出方程,完成解题。
●拓展演练
1.实践操作法
例1印刷一本书,为了使装订成书后页码恰好为连续的自然数,可按如下方法操作:如图10-8,先将一张整版的纸,对折一次为4页,再对折一次为8页,连续对折三次为16页,……;然后再排页码. 如果想设计一本16页的毕业纪念册,请你按图1、图2、图3(图中的1,16表示页码)的方法折叠,在图4中填上按这种折叠方法得到的各页在该面相应位置上的页码.
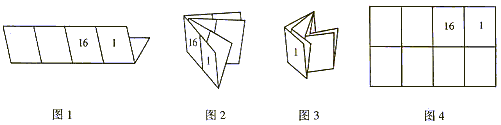
图10-8
解析:本题单凭想象完成有一定困难,但其实际操作较为简单,通过实际操作容易得到答案.
答案:
|
8 |
9 |
16 |
1 |
|
5 |
12 |
13 |
4 |
方法点拨:在考试时,完成这道题单凭想象完成比较困难,但却操作简单易行,建议考试时遇这类问题时,可进行实际操作.
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
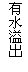

 ;
;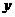 (
(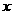 (个)之间的一次函数关系式(不要求写出自变量的取值范围);
(个)之间的一次函数关系式(不要求写出自变量的取值范围);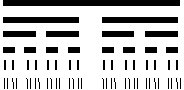

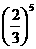 B.
B.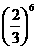 C.
C.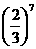 D.
D.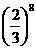


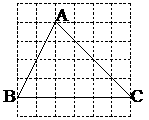
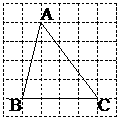
 例4如图10-6,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )
例4如图10-6,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为( )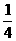 cm2 B.
cm2 B. cm2
cm2
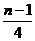 cm2 D.
cm2 D.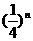 cm2
cm2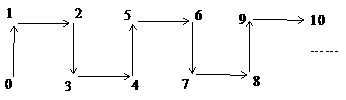
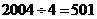 ,说明第2004个数刚好是完成第501个循环,同时又将开始下一个循环.
,说明第2004个数刚好是完成第501个循环,同时又将开始下一个循环.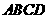 的边长
的边长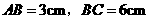 .某一时刻,动点
.某一时刻,动点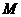 从
从 点出发沿
点出发沿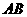 方向以
方向以 的速度向
的速度向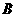 点匀速运动;同时,动点
点匀速运动;同时,动点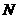 从
从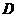 点出发沿
点出发沿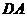 方向以
方向以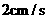 的速度向
的速度向 的面积等于矩形
的面积等于矩形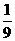 ?
?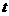 ,使以
,使以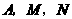 为顶点的三角形与
为顶点的三角形与 相似?若存在,求
相似?若存在,求


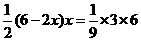 ,即
,即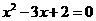 ,
,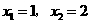 .
.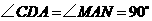 ,因此有
,因此有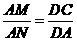 或
或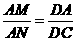
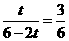 ①,或
①,或 ②.
②.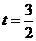 ;解②,得
;解②,得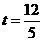
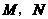 同时出发后,经过
同时出发后,经过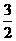 秒或
秒或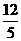 秒时,以
秒时,以