摘要：3．举一反三法 例4如图10-6.将n个边长都为1cm的正方形按如图所示摆放.点A1.A2.-.An分别是正方形的中心.则n个这样的正方形重叠部分的面积和为( ) A．cm2 B．cm2 C．cm2 D． cm2 解析:通过观察.不难发现.每两个连续的这样摆放的正方形中互相重叠的部分的面积刚好是一个正方形面积的四分之一.而三个连续这样摆放的正方形有两个这样的重叠的部分．所以n个这样的正方形重叠部分的面积和为 cm2 答案:选择C 方法点拨:归纳猜想题中.有许多试题是通过局部反映整体的．这时.要求能通过观察.发现这种特点.然后只需分析或者解决其中部分问题.再通过举一反三.达到通盘解决问题的目标．利用旋转或三角形全等知识可证明每两个相邻正方形重叠部分的面积等于一个正方形面积的四分之一.再通过观察.发现后面全部具有相同的规律.容易求出结果．
网址：http://m.1010jiajiao.com/timu3_id_468443[举报]
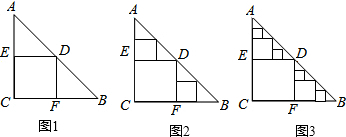
△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2．要在这张纸板中剪出一个尽可能大的正方形（剪法如图1所示），图1中剪法称为第1次剪取，记所得的正方形面积为S1；按照图1中的剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为S2（如图2），则S2=
；再在余下的四个三角形中，用同样的方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形的面积和为S3（如图3）；继续操作下去…则第10次剪取后，S10=
．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 29 |
| 1 |
| 29 |
某校为开展“阳光体育”运动，丰富学生课间自由活动内容，随机选取了本校100名学生进行调查，调查的内容是：你最喜欢的自由活动项目是什么？，将收集到的数据整理，给出了如图10所示的统计图．（1）学校采用的调查方法是
抽样调查法
抽样调查法
．（2）求“踢毽子”的人数，并在下图中将“踢毽子”部分的条形图补充完整．
（3）若该校有1600名学生，请估计喜欢“跳绳”的学生人数．
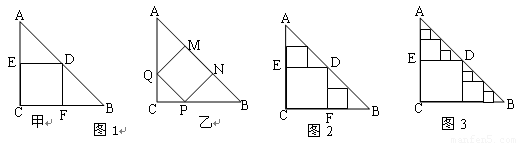
△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2，(1)要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法(如图1)，比较甲．乙两种剪法，哪种剪法所得的正方形面积大？请说明理由。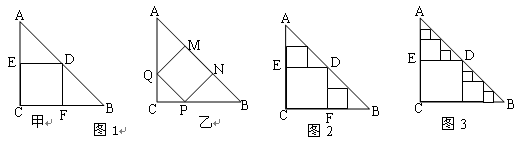
(2)图1中甲种剪法称为第1次剪取，记所得正方形面积为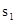
；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为
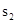(如图2)，则
；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为
，继续操作下去……，则第10次剪取时，
；
(3)求第10次剪取后，余下的所有小三角形的面积之和。
△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2，(1)要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法(如图1)，比较甲．乙两种剪法，哪种剪法所得的正方形面积大？请说明理由。
(2)图1中甲种剪法称为第1次剪取，记所得正方形面积为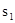
；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为
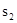(如图2)，则
；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为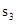
，继续操作下去……，则第10次剪取时，
；
(3)求第10次剪取后，余下的所有小三角形的面积之和。
查看习题详情和答案>>
