13、(2007河北省)一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部,B型手机y部.三款手机的进价和预售价如下表:
|
手机型号 |
A型 |
B型 |
C型 |
|
进 价(单位:元/部) |
900 |
1200 |
1100 |
|
预售价(单位:元/部) |
1200 |
1600 |
1300 |
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
解:(1)60-x-y;
(2)由题意,得 900x+1200y+1100(60-x-y)= 61000,整理得 y=2x-50.
(3)①由题意,得 P= 1200x+1600y+1300(60-x-y)- 61000-1500,
整理得 P=500x+500.
②购进C型手机部数为:60-x-y =110-3x.根据题意列不等式组,得
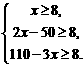 解得 29≤x≤34.
解得 29≤x≤34.
∴ x范围为29≤x≤34,且x为整数.(注:不指出x为整数不扣分)
∵P是x的一次函数,k=500>0,∴P随x的增大而增大.
∴当x取最大值34时,P有最大值,最大值为17500元.
此时购进A型手机34部,B型手机18部,C型手机8部.
11、(2007四川绵阳)绵阳市“全国文明村”江油白玉村果农王灿收获枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果全部运往外地销售,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)王灿如何安排甲、乙两种货车可一次性地运到销售地?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果农王灿应选择哪种方案,使运输费最少?最少运费是多少?
解:(1)设安排甲种货车x辆,则安排乙种货车(8-x)辆,依题意,得
4x + 2(8-x)≥20,且x + 2(8-x)≥12,
解此不等式组,得 x≥2,且 x≤4, 即 2≤x≤4.
∵ x是正整数, ∴ x可取的值为2,3,4.
因此安排甲、乙两种货车有三种方案:
|
|
甲种货车 |
乙种货车 |
|
方案一 |
2辆 |
6辆 |
|
方案二 |
3辆 |
5辆 |
|
方案三 |
4辆 |
4辆 |
(2)方案一所需运费 300×2 + 240×6 = 2040元;
方案二所需运费 300×3 + 240×5 = 2100元;
方案三所需运费 300×4 + 240×4 = 2160元.
所以王灿应选择方案一运费最少,最少运费是2040元.
10、(2007南充)某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机的进货量的一半.电视机与洗衣机的进价和售价如下表:
|
类 别 |
电视机 |
洗衣机 |
|
进价(元/台) |
1800 |
1500 |
|
售价(元/台) |
2000 |
1600 |
计划购进电视机和洗衣机共100台,商店最多可筹集资金161 800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其它费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
解:(1)设商店购进电视机x台,则购进洗衣机(100-x)台,根据题意,得
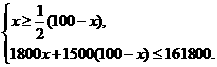 ,解不等式组,得
,解不等式组,得 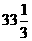 ≤x≤
≤x≤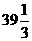 .
即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得
y=(2000-1800)x+(1600-1500)(100-x)=100x+10000.
∵ 100>0,∴ 当x最大时,y的值最大.
即 当x=39时,商店获利最多为13900元
.
即购进电视机最少34台,最多39台,商店有6种进货方案.
(2)设商店销售完毕后获利为y元,根据题意,得
y=(2000-1800)x+(1600-1500)(100-x)=100x+10000.
∵ 100>0,∴ 当x最大时,y的值最大.
即 当x=39时,商店获利最多为13900元
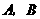 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个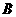 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.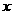 个,则
个,则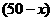 个,依题意,得:
个,依题意,得: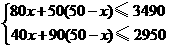 ,解这个不等式组,得:
,解这个不等式组,得: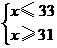 ,
,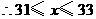
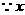 是整数,
是整数,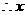 可取
可取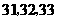 ,
, 可设计三种搭配方案:
可设计三种搭配方案: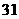 个
个 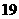 个
个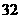 个
个 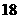 个
个 个
个 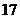 个.
个. 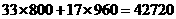 (元)
(元)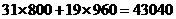 (元)
(元)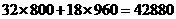 (元)
(元)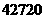 元
元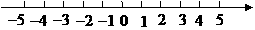 (2007上海)解不等式组:
(2007上海)解不等式组: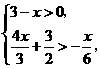 并把解集在数轴上表示出来.
并把解集在数轴上表示出来.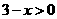 ,解得
,解得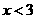 .
. 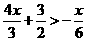 ,解得
,解得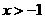 .
. 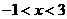 .
. 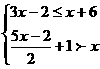 ,并把其解集在数轴上表示出来。
,并把其解集在数轴上表示出来。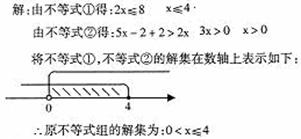
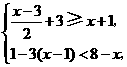 并写出该不等式组的整数解
并写出该不等式组的整数解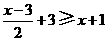 ,得
,得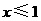 .
.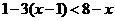 ,得
,得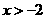 .
. 原不等式组的解集是
原不等式组的解集是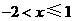 .
.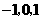 .
.