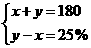题型一 方程组解的判定
例1已知二元一次方程组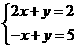 的解是( )
的解是( )
A.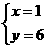 B.
B.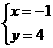 C.
C.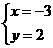 D.
D.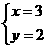
分析:本题有两种解法:一种是解方程组,求出其解;另一种是将被选答案代入方程组,逐个验证。
答案:B
题型二 求待定系数或代数式的值
例2已知二元一次方程组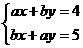 的解是
的解是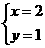 ,则a+b的值为________。
,则a+b的值为________。
分析:根据方程组的定义,把x=2,y=1代入方程组,转化为关于a、b的方程组,解出a与b的值,问题就解决了,也可应用整体思想,直接求出a+b的值。
解法1:把x=2,y=1代入方程组,
得 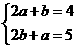 解得
解得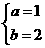
∴a+b=3
解法2:把x=2,y=1代入原方程组,
得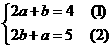
(1)+(2)得3(a+b)=9,∴a+b=3
点评:运用整体思想巧求代数式的值是中考常考内容,解题时,注意观察方程组的特点,灵活运用方程组的变形技巧而进行合理、正确的解答。
|
例3 解方程组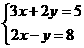
分析:因为y的系数绝对值是1,所以用代入消元法解较简单。
解:由②,得y=2x-8 ③
把③代入①,得3x+2(2x-8)=5
3x+4x-16=5
∴x=3
把x=3代入③,得y=2×3-8=-2
∴方程组的解为 x=3 y=-2
点评:解方程组要善于观察方程组的特点,灵活选用适当的方法,提高解题速度。
题型四 列方程组解应用题
例4某山区有23名中、小学生因贫困失学需要捐助, 资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
|
|
初一年级 |
初二年级 |
初三年级 |
|
捐款数额(元) |
4000 |
4200 |
7400 |
|
捐助贫困学生(名) |
2 |
3 |
|
|
捐助贫困小学生人数(名) |
4 |
3 |
|
(1)求a、b的值;
(2)初三年级学生的捐款解决了其余贫困中小学生的学习费用, 请将初三年级学生可捐助的贫困中、小学生人数直接填入上表中。(不需写出计算过程)
分析:本题存在两个等量关系,分别是捐助2名中学生的学习费用+4 名小学生的学习费用=4000和捐助3名中学生的学习费用+3名小学生的学习费用=4200。
解:(1)根据题意,得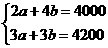
解这个方程组,得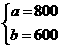
(2)初三年级学习捐助贫困中学生人数为4(名), 捐助贫困小学生人数为7(名)。
基础达标验收卷
|
考点 |
课标要求 |
知识与技能目标 |
|||
|
了解 |
理解 |
掌握 |
灵活应用 |
||
|
二元一次方程组 |
了解二元一次方程(组)及解的定义 |
∨ |
|
|
|
|
熟练掌握用代入法和加减法解二元一次方程组的方法并能灵活运用 |
|
∨ |
∨ |
∨ |
|
|
能正确列出二元一次方程组解应用题 |
|
|
∨ |
∨ |
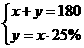 B.
B.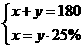 ; C.
; C.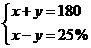 D.
D.